경우의 수
표본공간에서 사건 A가 발생할 확률

팩토리얼(!)
1부터 어떤 양의 정수 n까지의 정수를 모두 곱한 것
0! = 1
1! = 1
n! = n * (n-1)!
# ! 함수 정의
def fac(n):
if n == 0:
return 1
else:
return n * fac(n-1)
# 4! 계산
print(fac(4))
공리
증명을 필요로 하지 않거나 증명할 수 없지만 직관적으로 자명한 진리인 명제
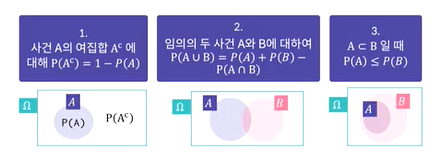
-모든 사건 A에 대하여 0 <= P(A) <= 1
-표본공간에 대해 P(표본공간) = 1

확률의 정리
순열
곱의 법칙에 의해 총 가능한 경우의 수 = n개의 서로 다른 원소 중 k개를 선택하여 배열하는 경우의 수
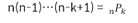
from itertools import permutations
list(permutations([n], k))서로 다른 n개의 원소를 주고, 이 원소들 중 k개를 순서를 고려하여 뽑는 경우의 수 계산
#순열
from itertools import permutations
from itertools import combinations
# 순열: 6명 수강생 중 2명에게 순위별 상품을 주는 경우의 수
rank_per = list(permutations(["가", "나", "다", "라", "마", "바"], 2))
rank_per_num = len(rank_per)
print(rank_per)
print(rank_per_num)
조합
서로 다른 n개의 원소에서 k개를 순서에 상관없이 선택하는 방법

순열: 순서가 있음
조합: 순서가 없음
#조합
from itertools import permutations
from itertools import combinations
# 조합: 6명 수강생 중 2명에게 순위 상관없이 상품을 주는 경우의 수
rank_com = list(combinations(["가", "나", "다", "라", "마", "바"], 2))
rank_com_num = len(rank_com)
print(rank_com)
print(rank_com_num)
중복순열
서로 다른 n개의 원소 중에서 중복을 허용하여 r개를 뽑아 일렬로 배열하는 경우

from itertools import product
list(product[n], repeak = k)#중복순열
from itertools import product
from itertools import combinations_with_replacement
# 중복순열
re_per = list(product(["A", "B", "C", "D", "E"], repeat=3))
re_per_num = len(re_per)
print(re_per)
print(re_per_num)
중복조합
서로 다른 N개의 대상 중 중복을 허용해 r개를 순서를 고려하지 않고 뽑는 경우

#중복조합
from itertools import product
from itertools import combinations_with_replacement
# 중복조합
re_com = list(combinations_with_replacement(["A", "B", "C", "D", "E"], 3))
re_com_num = len(re_com)
print(re_com)
print(re_com_num)
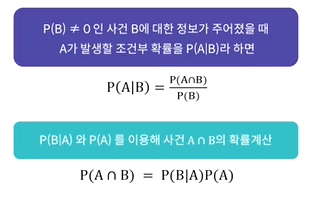
조건부확률
특정한 사건의 확률을 구할 때, 다른 사건에 대한 정보가 주어지는 경우
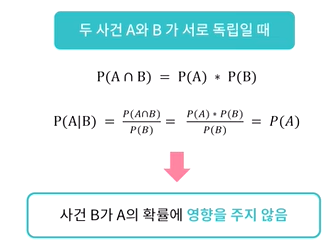
독립
일반적으로 두 사건은 서로 연관성이 있는 경우가 많음
조건부 확률은 두 사건의 연관성에 따라 달라진다

#조건부 확률과 독립
import random
answer_Q1andQ2 = 0
answer_Q2 = 0
answer_Q1orQ2 = 0
random.seed(4)
# 함수 정의
def random_answer():
return random.choice(["A", "B"])
# 30명의 응답 결과
for i in range(30):
Q1 = random_answer()
Q2 = random_answer()
if Q2 == "A":
answer_Q2 += 1
if Q2 == "A" and Q1 == "A":
answer_Q1andQ2 += 1
if Q2 == "A" or Q1 == "A":
answer_Q1orQ2 += 1
# 조건부 확률과 독립
print( "P(Q1 and Q2 | Q2 ):", answer_Q1andQ2 / answer_Q2)
print( "P(Q1 and Q2 | Q1 or Q2 ):", answer_Q1andQ2 / answer_Q1orQ2)
확률변수
각각의 근원사건에 실수값을 대응시킨 함수
대문자로 표시
시행을 하기 전엔 어떤 값을 갖게 될 지 알 수 없다는 불확실성을 표현
이산확률분포
이산확률변수: 확률변수의 값의 개수를 셀 수 있는 경우
연속확률변수: 확률변수의 값이 연속적인 구간에 속하는 경우
→ 합계 1
확률질량함수
어떤 확률변수 x가 갖는 확률을 나타내는 함수
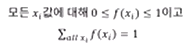
이산확률분포
베르누이, 이항, 기하, 음이항, 초기하, 포아송 분포 등
확률밀도함수
연속확률변수X가 갖는 확률의 분포를 표현
연속확률분포

균일, 지수, 감마, 정규, 베타 분포 등
누적분포함수

X가 가질 수 있는 가장 작은 값부터 X까지 해당하는 확률질량함수의 값을 누적해서 더한 것
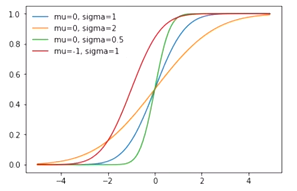
#확률변수
from sympy.stats import given, density, Die
# Q1. 6개의 면이 있는 주사위 생성
Die6 = Die("Die6", 6)
Die6_dict = density(Die6).dict
print(Die6)
print(Die6_dict)
# Q2. 3 초과의 면만 나오는 조건을 가진 주사위 생성
condi = given(Die6, Die6 > 3)
condi_dict = density(condi).dict
print(condi)
print(condi_dict)'[데이터분석] > Python | AI | 머신러닝' 카테고리의 다른 글
| Regression Problem (0) | 2024.09.09 |
|---|---|
| Python을 활용한 프로그래밍 확률통계_Part 4 (0) | 2024.08.01 |
| 현업 문제해결 유형별 머신러닝 알고리즘 Part 1 (0) | 2024.07.29 |
| 실무 중심의 데이터 분석 방법 Part.4 (0) | 2024.07.29 |
| Python을 활용한 프로그래밍 확률통계_Part 2 (0) | 2024.07.29 |