Error = Variance + Bias
variance: 추정 값(Algorithm Output)의 평균과 추정 값 (Algorithm Output) 들 간의 차이
bias: 추정 값 (Algorithm Output)의 평균과 참 값 (True) 들 간의 차이
bias는 참 값과 추정 값의 거리를 의미
variance는 추정 값들의 흩어진 정도를 의미


Error = Noise (Data) + Variance + Bias
Simple Linear Regression
독립변수 X 1개, 종속변수 Y 1개
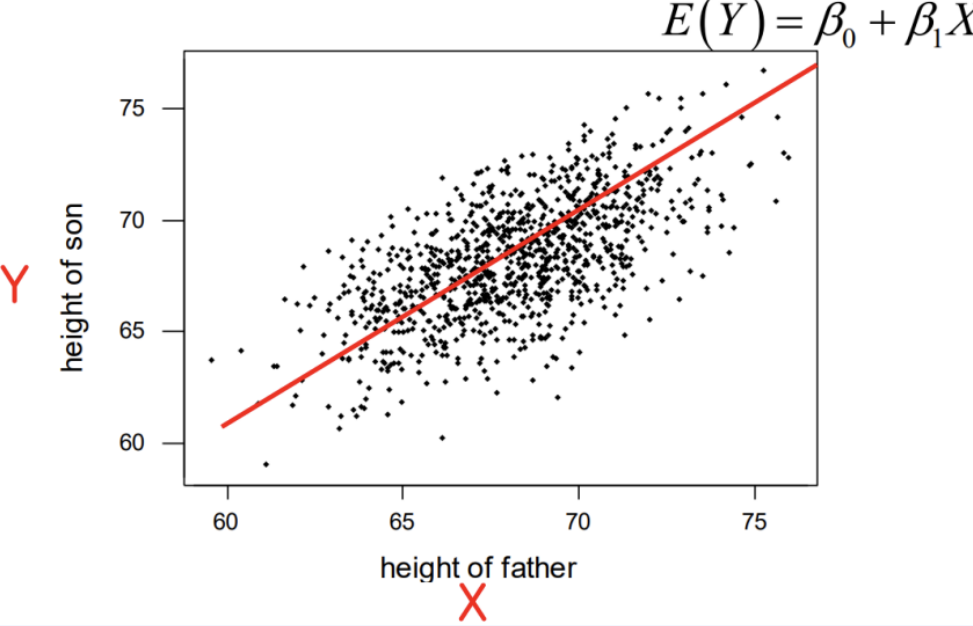
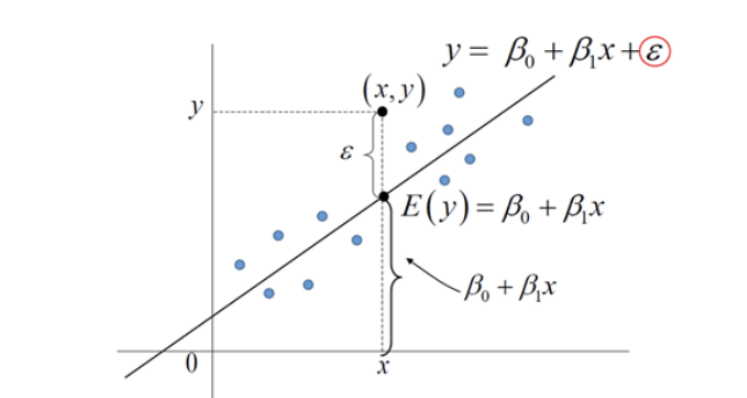
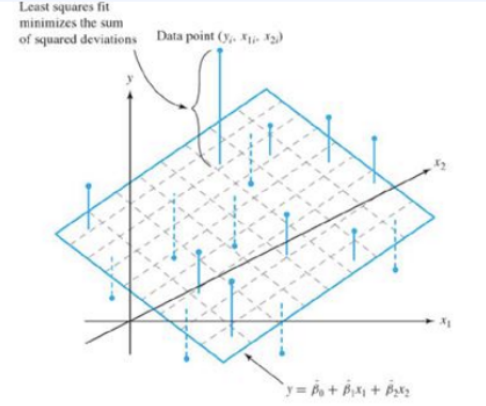
Multi Linear Regression
독립변수 X 여러 개, 종속변수 Y 1개
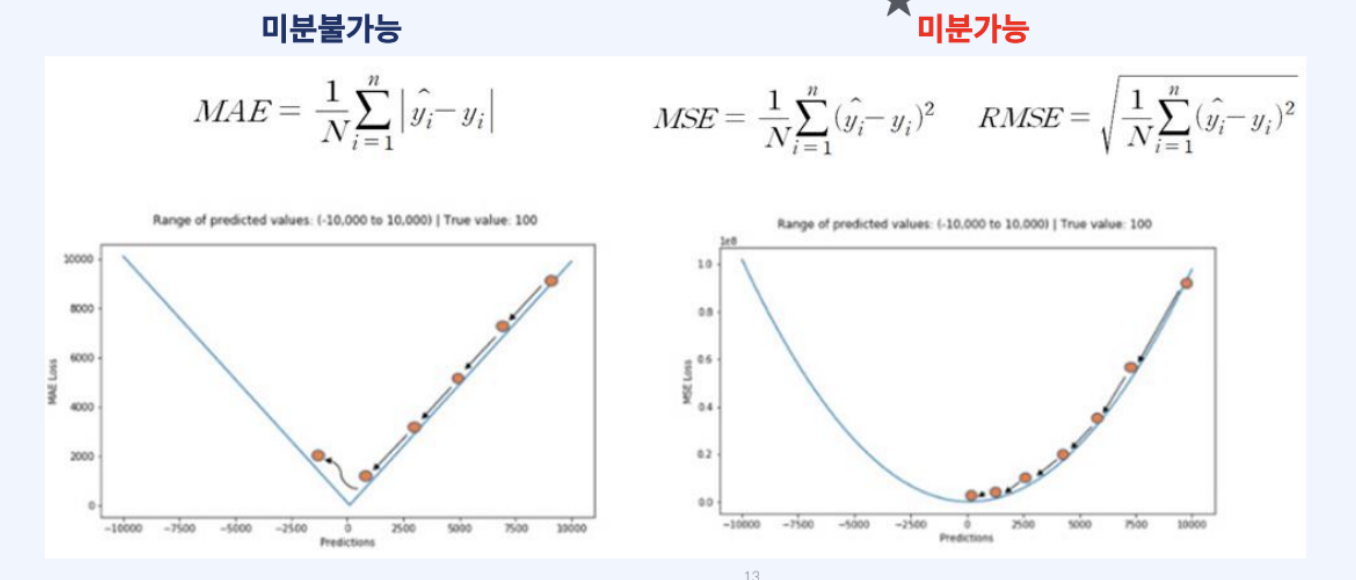
Why use Square?
미분 가능
β 추정법
각 β에 대해 편미분을 사용하여 추정
Linear Regression의 Loss Function은 Closed Form Quadratic이기 때문에 미분만으로 쉽게 추정 가능

추정한 β에 대해 검증을 수행
β에 대한 p-value가 낮으면 기울기가 0이 아닌 것으로 판명
(통상적으로 p-value가 0.05 이하면 의미 있다고 판단. β의 기울기가 0일 확률이 0.05 이하라고 해석)
p-value <= 0.05: H0 (귀무가설) 기각 H1 채택
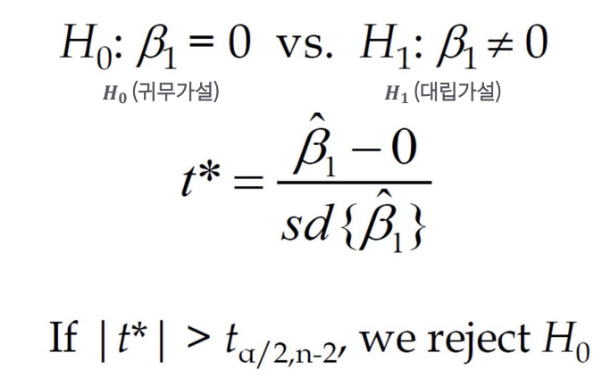
Factor 1: βi의 값이 크면 Y에 영퍙을 크게 미친다고 판단할 수 있음
그러나 X's 간 Scale이 다를 수 있기 때문에 X's 간 상대적인 비교는 불가능함
(eg. 키와 몸무게는 Scale이 다름)
Factor 2: p-value
βi 값이 크지만 p-value 값이 높으면 의미가 없음
→ βi와 p-value 값, 두 가지 조건이 맞아야 유의미하다고 할 수 있음
→ X's 간 중요한 변수를 Ranking하고 싶을 때 다른 방법이 있는가?
Model 성능에 대한 평가 기준
: 동일한 평가 기준으로 Model의 성능을 평가해야 함
R2 (R-square)
Regression Model의 정성적인 적합도 판단
: 평균으로 예측한 것에 대비 분산을 얼마나 축소 시켰는지에 대한 판단
: 0 - 1 사이의 값을 가지며 1에 가까울 수록 좋은 모델
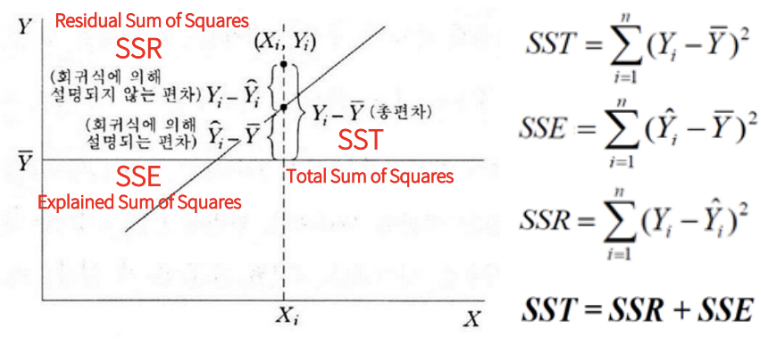

: 현업에서 0.3 이상인 경우를 찾기 힘듦
: R-square의 경우 0.25 정도도 유의미하다고 판단
Average Error 평균오차
: 실제 값에 비해 과대/과소 추정 여부를 판단
: 부호로 인해 잘못된 결론을 내릴 위험이 있음
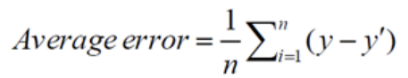
MAE (Mean Absolute Error) 평균 절대 오차
: 실제 값과 예측 값 사이의 절대적인 오차의 평균을 이용
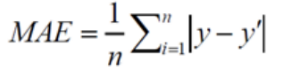
MAPE (Mean Absolute Percentage Error) 평균 절대 비율 오차
: 실제값 대비 얼마나 예측 값이 차이가 있는지 %로 표현
: 상대적인 오차를 추정하는데 주로 사용
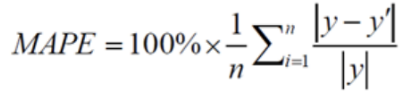
RMSE (Root Mean Squared Error)
: 부호의 영향을 제거하기 위해 절대값이 아닌 제곱을 취한 지표
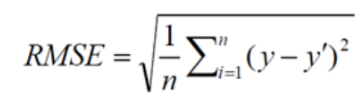
Model Loss Function은 평가지료로 하는 것이 좋음
Model 성능 체크: 정성, 정량
p-value를 확인하여 의미 있는 변수 추출
βi 활용, X 1단위 증가 당 Y에 얼마 만큼 영향을 미치는지 판단
Feature Selection
Overfitting을 방지하기 위해서 수행
Feature의 수가 많아지면 많아질수록 Model Complexity (복잡도) 는 높아짐
Model Complexity가 높아지면 높아질 수록 Bias는 낮아지는 반면 Variance가 높아짐
Error(X) = Noise(X) + Bias(X) + Variance(X)
Feature Selection 기법
Supervised Variable Selection - Exhaustive Search (완전 탐색)
: 경우의 수는 2^p - 1 (p는 Feature의 갯수)
: Training Set의 정확도 보다 Test Set의 정확도를 봄
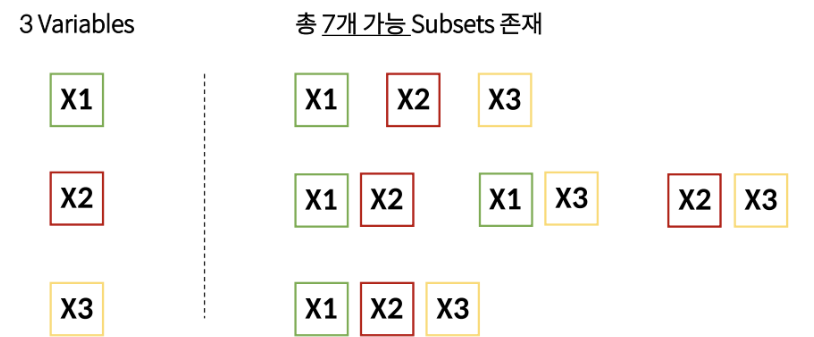
: 완전탐색 방법은 시간이 너무 오래 걸림
: 시간이 Exponential(지수) 하게 증가



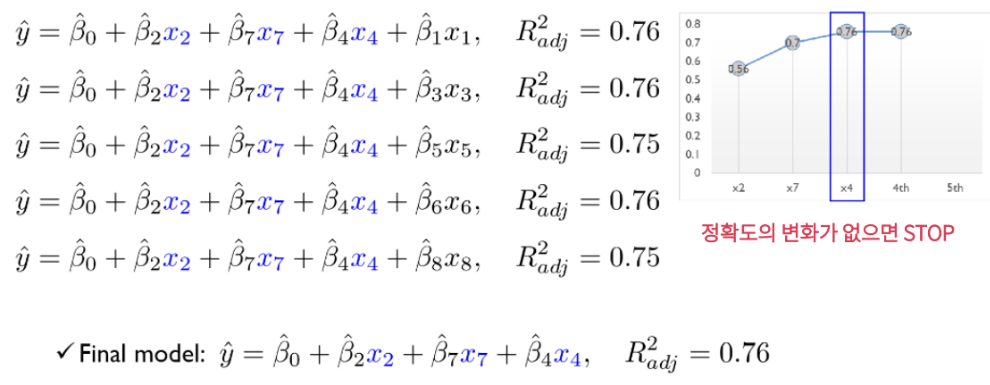
Supervised Variable Selection - Forward Selection
: 처음에는 variable이 없이 시작해서 하나씩 중요한 변수들을 Sequentially 추가함
: 한 번 선택된 variable은 절대 지우지 않음
Supervised Variable Selection - Backward Elimination
: Multiple linear Regression에서의 Backward Elimination


: 처음에는 모든 variables을 사용하고, 정확도에 영향을 미치지 않는 불필요한 variable을 sequentially 제거함
: 한 번 제거된 variable은 절대 다시 선택하지 않음
Supervised Variable Selection - Stepwise Selection
: Forward Selection과 Backward Elimination을 번갈아 가며 수행함
: 시간이 오래 걸릴 수 있지만, 최적 Variable Subsed을 찾을 가능성이 높음

R-square는 회귀 분석에서 모델이 데이터의 변동을 얼마나 잘 설명하는지를 나타내는 지표입니다. R-square 값은 0에서 1 사이의 값을 가지며, 1에 가까울수록 모델이 데이터의 변동을 더 잘 설명한다는 의미입니다. 즉, R-square 값이 클수록 모델이 독립 변수가 종속 변수의 변화를 잘 예측하고 있다는 것을 나타냅니다.
하지만 R-square 값이 높다고 해서 항상 모델이 좋은 것은 아닙니다. 과적합(overfitting)이 발생할 수 있으며, 모델의 복잡성이나 다른 통계적 지표도 함께 고려해야 합니다. R-square 값은 모델 평가의 하나의 요소일 뿐입니다.
Penalty Team
전통적인 Feature Selection의 단점
: Variables가 커짐에 따라 시간이 매우 오래 걸림
: 가성비가 떨어짐
→ Model이 Error를 Minimize 하는 과정에서 Feature을 Selection 해줄 수 있는 방법은 없을까?
Feature Selection의 종류
1. Filter Method
X's와 Y의 Correlation, Chi-Square Test, Anova, Variance Inflation Factor 등 간단한 기법으로 Filtering 수행
2. Wrapper Method
Forward Selection, Backward Elimination, Stepwise Selection을 활용한 Feature selection
3. Embedded Method
Regularization Approach를 활용하여 Model이 스스로 Feature Selection을 진행하는 방법
Embedded Method의 장점
: Wrapper Method와 같이 Features의 상호작용을 고려함
: 다른 방법보다 상대적으로 시간을 절약할 수 있음
: Model이 Train하면서 Feature의 Subset을 찾아감
Penalty Team
: Model에서는 불필요한 Feature에게 '벌'을 부여햐여 학습하지 못하게 함
: Error를 Minimize하는 제약 조건에서는 필요 없는 Feature의 β(계수)에 Penalty를 부여함
Regularized Model - Ridge
β^2에 Penalty Term을 부여하는 방식
Regularized Model의 경우 Feature간 Scaling 필수


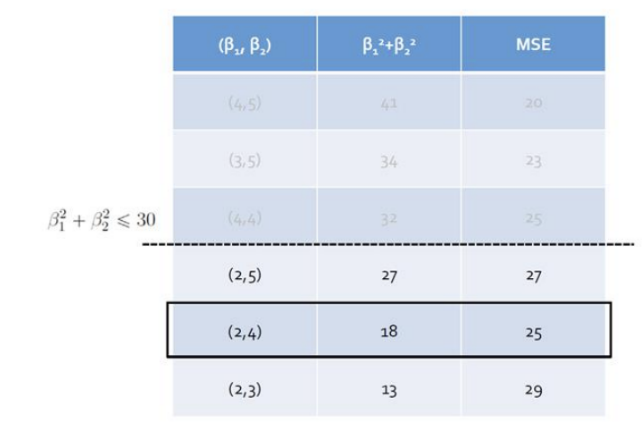
Ridge Regression
: β^2에 Penalty Term을 부여하는 방식 = L2 - norm = L2 Regression
: 제곱 오차를 최소화하면서 회귀 계수 β^2을 제한함

: MSE Contour
중심에서 멀어질수록 Error 증가 → Train Error를 조금 증가시키는 과정 (Overfitting 방지)
Ridge Estimator와 MSE Contour가 만나는 점이 제약 조건을 만족하며 Error가 최소가 됨
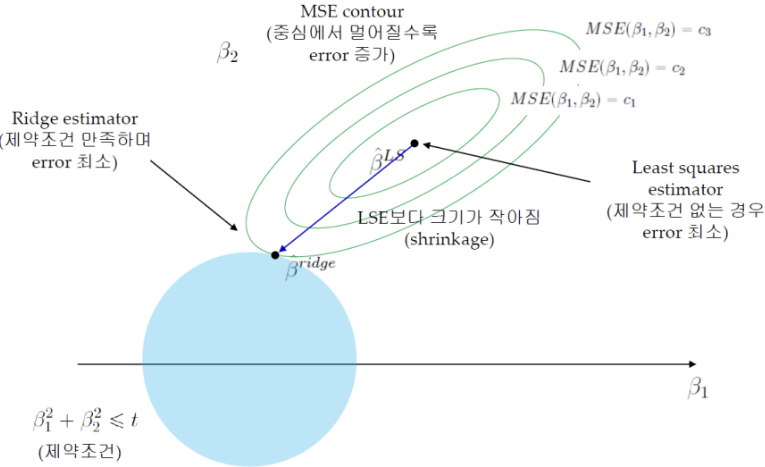
이 그림은 Ridge 회귀 분석을 설명하는 그림입니다. Ridge 회귀는 회귀 분석에서 **과적합(overfitting)**을 방지하기 위해 사용되는 기법입니다. 여기서 과적합은 모델이 학습 데이터에 너무 맞춰져서 새로운 데이터에 대한 일반화 성능이 떨어지는 경우를 말합니다.


Ridge는 미분이 가능하기 때문에 Closed Form solution을 구할 수 있음
빠르게 해를 찾을 수 있음

Ridge Regression 특징
: Ridge는 해 공간에서도 볼 수 있듯 Feature Selection은 되지 않음
: 하지만 불필요한 Feature는 충분히 0에 수렴하게 만들어버림
: Ridge Regression은 Feature의 크기가 결과에 큰 영향을 미치기 때문에 Scaling이 중요함
: 다중공선성 Multicollinearity 방지에 가장 많이 쓰임
LASSO Regression
Least Absolute Shrinkage and Selection Operator
|β| = L1 - norm = L1 Regularization에 Penalty Term을 부여하는 방식
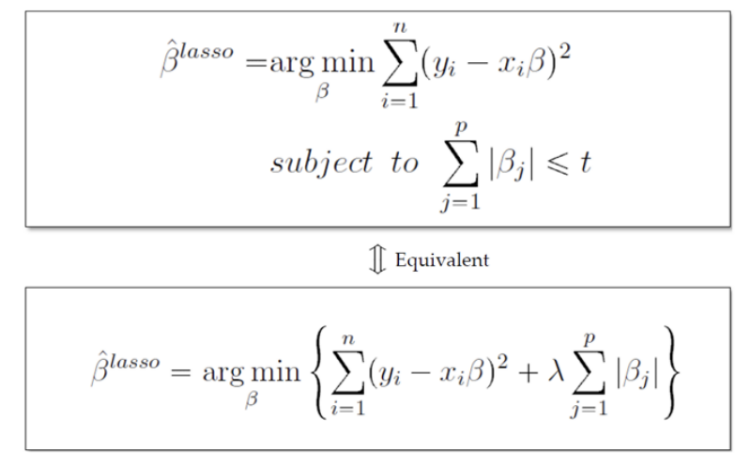
: MSE Contour: 중심에서 멀어질수록 Error 증가 → Train Error를 조금 증가시키는 과정 Overfitting 방지
: Ridge Estimator와 MSE Contour가 만나는 점이 제약 조건을 만족하며 Error가 최소가 됨
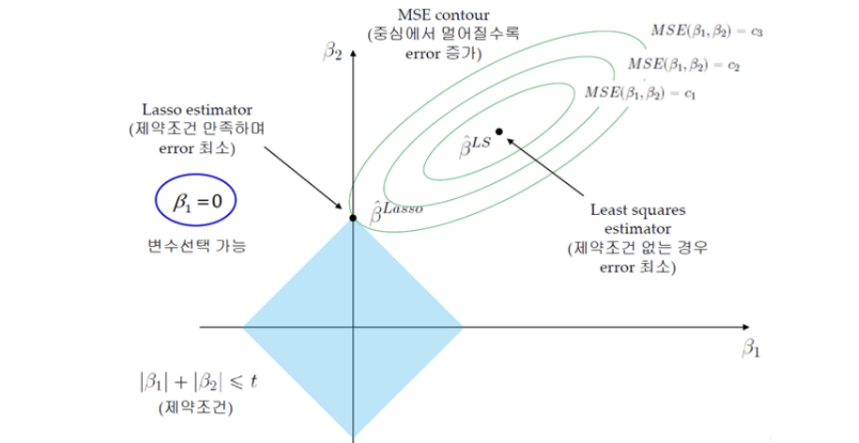
: Ridge Regression과 달리 Lasso Formulation은 Closed Form Solution을 구하는 것이 불가능
(절대값이기 때문에 미분 불가능)
: Numerical Optimization Methods 필요
- Quadratic Programming techniques
- LARS Algorithm
- Coordinate descent Algorithm
- Semi-differentiable
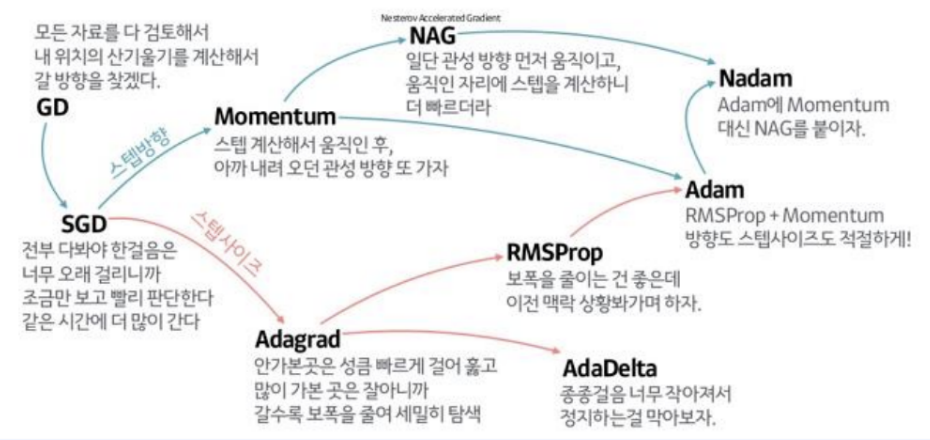
: Gradient Descent 경사 하강법
- Non-convex 경우 Grdient Descent를 활용하여 해 (Loss가 가장 낮은) 를 찾아감
- 대부분의 non-linear regression 문제는 closed form solution이 존재하지 않음
- Closed form solution이 존재해도 수많은 parameter가 있을 때 Gradient Descent로 해결하는 것이 효율적
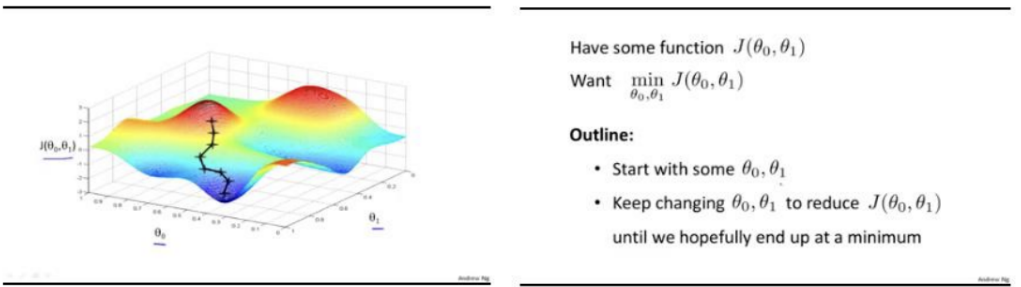
- Gradient Descent의 경우 최적해를 보장할 수 없음
- 그러나 복잡한 여러 해들이 존재할 때 가장 유용한 방법
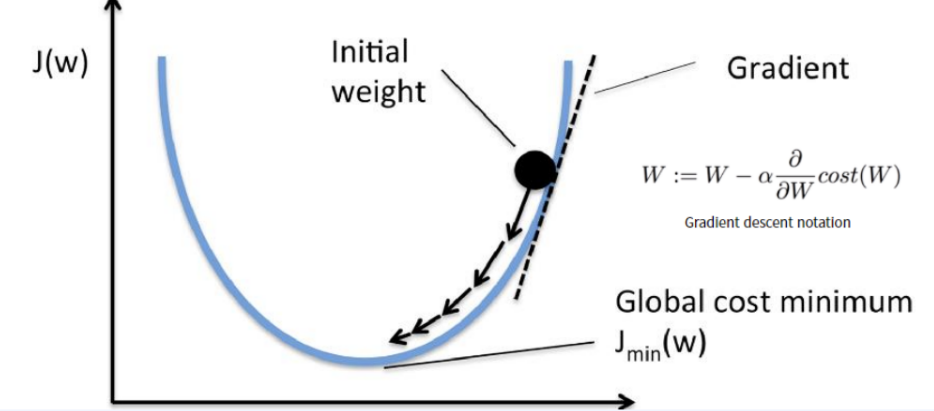
- Local Minima에 빠질 수 있음
- Global Minimum이 있는지 알 수 없음
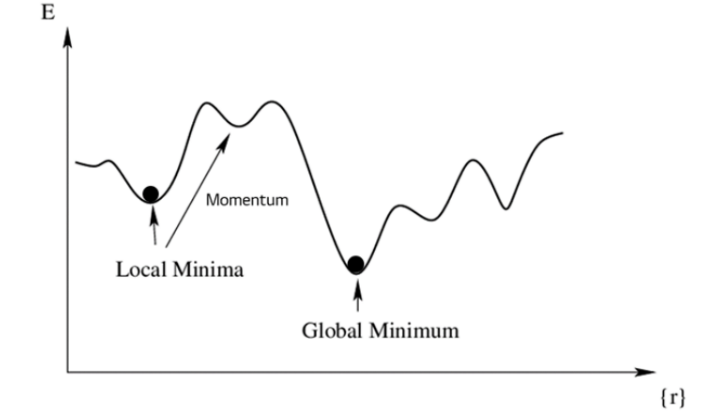
Local Minima에서 빠져나오기 위해 Momentum이라는 변수를 사용함
어느 정도 하강 시 다른 곳으로 튀어 버리면서 Local Minima를 빠져 나옴
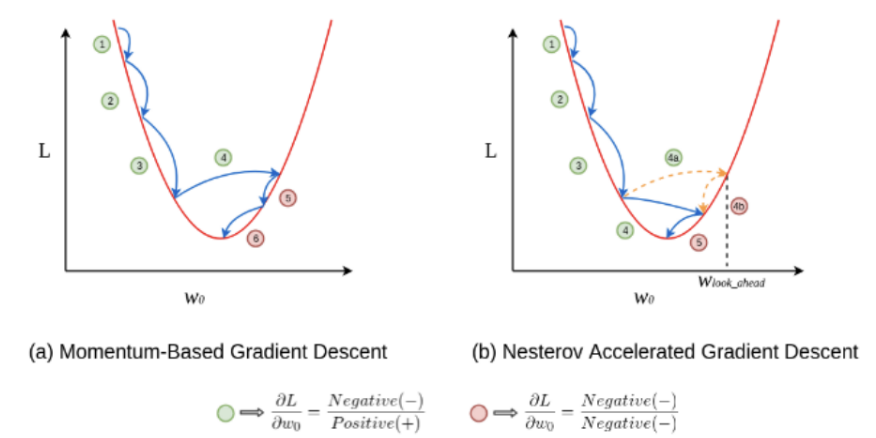
LASSO Regression
: Ridge Regression과 달리 Lasso Formulation은 Closed Form Solution을 구하는 것이 불가능
: 절대값이기 때문에 미분 불가능

Ridge와 LASSO 모두 t가 작아짐에 따라 ( λ가 커짐에 따라) 모든 계수의 크기가 감소함
Ridge: 크기가 큰 변수가 더 빠르게 감소하는 경향을 보임
LASSO: 예측에 중요하지 않은 변수가 더 빠르게 감소, t가 작아짐에 따라 예측에 중요하지 않은 변수는 0이 됨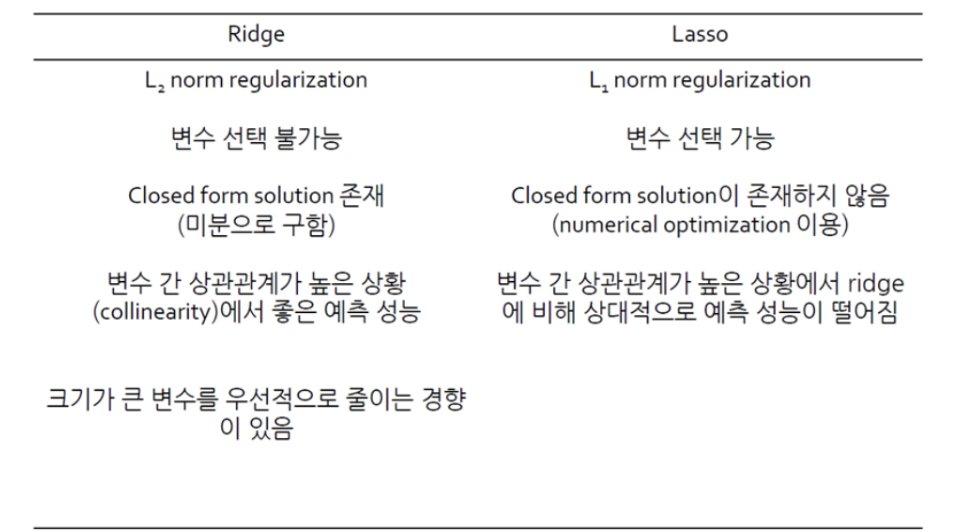
이 그림은 Ridge 회귀와 Lasso 회귀의 차이점을 비교하고 있습니다. 두 방법 모두 회귀 분석에서 정규화(regularization) 기법을 사용하여 과적합을 방지하는 데 도움을 줍니다. 하지만 사용하는 정규화 방식과 그에 따른 특징이 다릅니다. 이를 하나씩 설명하겠습니다.
1. Ridge 회귀
- L2 norm regularization: Ridge 회귀는 L2 정규화를 사용합니다. 이는 모델의 계수들의 제곱합을 최소화하는 방식으로, 회귀 계수가 너무 커지는 것을 방지합니다.
- 변수 선택 불가능: Ridge 회귀는 모든 변수들을 유지하면서 각 계수의 크기를 줄입니다. 즉, 중요하지 않은 변수의 계수도 0이 되지 않고, 어느 정도의 값을 가질 수 있습니다. 따라서 변수를 완전히 제거하지 않습니다.
- Closed form solution 존재: Ridge 회귀는 수학적으로 미분 가능한 closed form solution이 존재합니다. 이는 명확한 수식을 통해 해를 직접 구할 수 있다는 뜻입니다.
- 변수 간 상관관계가 높은 상황에서 좋은 성능: Ridge 회귀는 독립 변수들 간에 상관관계가 높을 때도 잘 작동합니다. 상관관계가 높은 변수들이 있어도 Ridge는 이를 적절히 처리하면서 모델을 안정적으로 만듭니다.
- 크기가 큰 변수를 우선적으로 줄이는 경향: Ridge 회귀는 회귀 계수의 크기가 큰 변수들을 먼저 줄이는 경향이 있습니다. 즉, 더 큰 영향을 미치는 변수들의 계수를 우선적으로 작게 만듭니다.
2. Lasso 회귀
- L1 norm regularization: Lasso 회귀는 L1 정규화를 사용합니다. 이는 계수들의 절댓값 합을 최소화하는 방식입니다.
- 변수 선택 가능: Lasso 회귀는 일부 회귀 계수를 0으로 만들 수 있습니다. 즉, 덜 중요한 변수를 제거하고 중요한 변수만을 선택하는 역할을 할 수 있습니다. 이를 통해 **변수 선택(feature selection)**이 가능합니다.
- Closed form solution이 존재하지 않음: Lasso 회귀는 미분 가능한 closed form solution이 존재하지 않습니다. 따라서 수치 최적화(numerical optimization)를 사용하여 해를 구해야 합니다.
- 변수 간 상관관계가 높은 상황에서 성능 저하: Lasso 회귀는 독립 변수 간에 상관관계가 높을 때 Ridge에 비해 예측 성능이 떨어질 수 있습니다. 상관관계가 높은 변수들 중 일부를 0으로 만들 수 있기 때문에 문제가 발생할 수 있습니다.
- 변수를 완전히 제거할 수 있음: Lasso는 중요하지 않은 변수들의 계수를 0으로 만들어 해당 변수를 제거할 수 있습니다. 즉, 변수 선택이 가능합니다.
정리
- Ridge 회귀는 모든 변수를 유지하면서 계수들의 크기를 줄이는 방식으로 과적합을 방지하며, 상관관계가 높은 변수들 간의 문제도 잘 해결합니다.
- Lasso 회귀는 중요한 변수만을 선택하고 나머지 변수들은 제거하는 방식으로 과적합을 방지하며, 변수 선택 기능이 있습니다.
따라서, Ridge는 변수를 모두 유지하며 과적합을 줄이는 데 적합하고, Lasso는 변수를 선택하는 데 강점이 있지만 상관관계가 높은 변수들 간에는 예측 성능이 떨어질 수 있습니다.
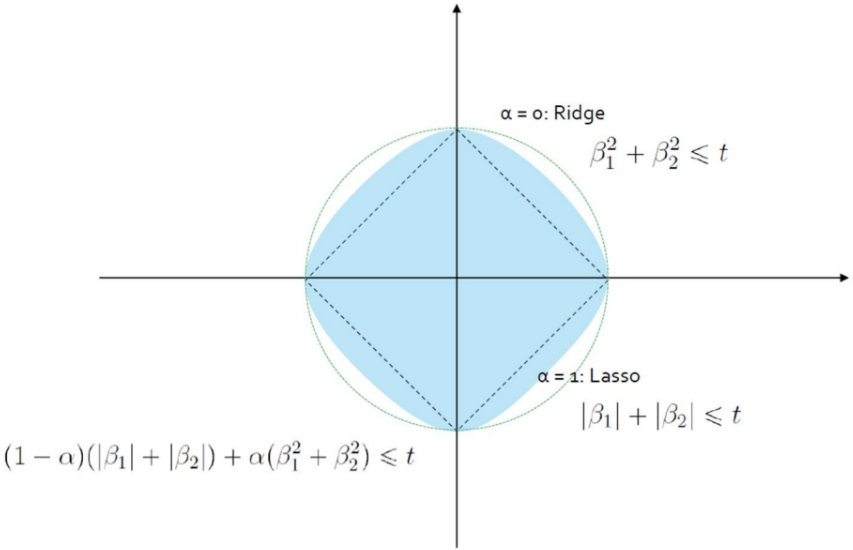
Ridge + LASSO = ElasticNet
ElasticNet은 Ridge의 L1-norm과 LASSO의 L2-norm을 섞음

λ1: LASSO Penalty Term (Feature Selection)
λ2: Ridge Penalty Term (다중공선성 방지)
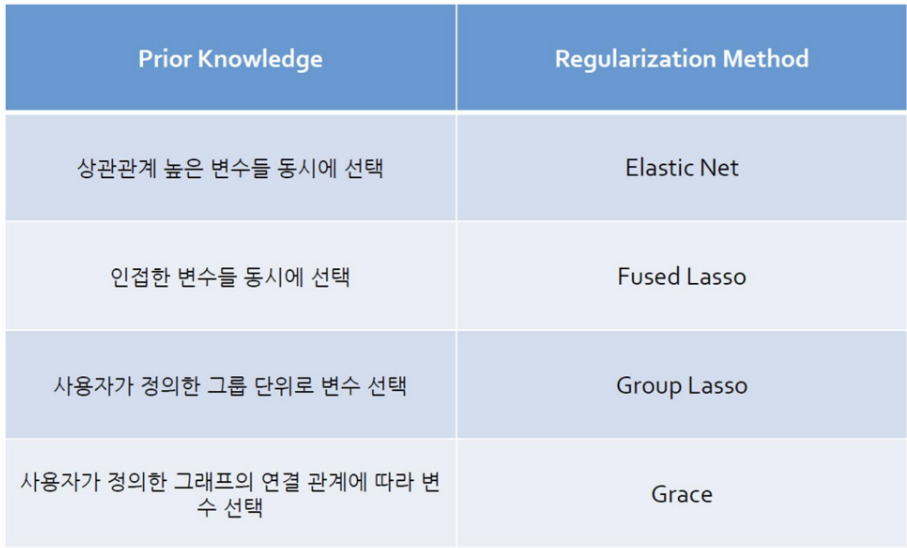
ElasticNet은 Correlation이 강한 변수를 동시에 선택 / 배제하는 특징을 가지고 있음
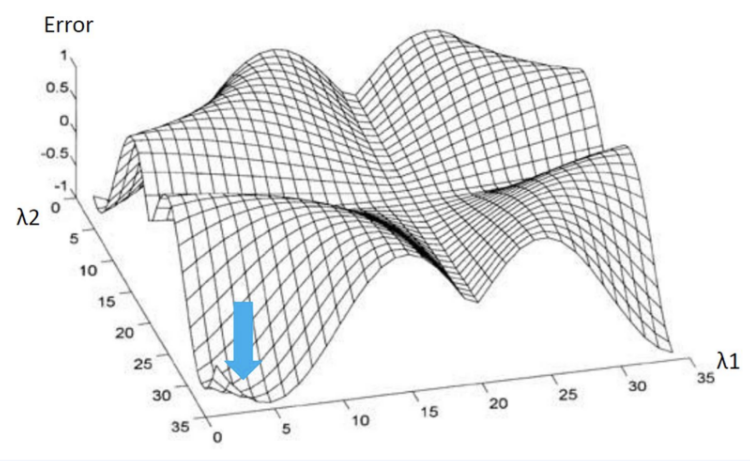
일정 범위 내로 λ1, λ2를 조정하여 가장 좋은 예측 결과를 보이는 λ1, λ2를 선정함
Ridge, LASSO보다 더 많은 실험이 필요하다는 단점이 존재
'[데이터분석] > Python | AI | 머신러닝' 카테고리의 다른 글
| eXplainableMethod (1) | 2024.09.16 |
|---|---|
| Classification Problem (0) | 2024.09.10 |
| Python을 활용한 프로그래밍 확률통계_Part 4 (0) | 2024.08.01 |
| Python을 활용한 프로그래밍 확률통계_Part 3 (0) | 2024.07.30 |
| 현업 문제해결 유형별 머신러닝 알고리즘 Part 1 (0) | 2024.07.29 |