확률분포
이산확률분포
확률 변수의 값이 정수와 같이 이산적인 값을 가진 경우
-베르누이 분포
베르누이 시행
1) 각 시행은 성공과 실패 두 가지 중 하나의 결과를 가짐
2) 각 시행에서 성공할 확률: p 실패할 확률: 1-p
3) 각 시행은 서로 독립으로 각 시행의 결과가 다른 시행의 결과에 영향을 미치지 않음

-이항분포
베르누이 시행을 반복했을 때, 성공하는 횟수의 확률분포
이항실험: 성공확률이 동일한 베르누이 시행을 독립적으로 반복하는 실험
이항확률변수: 전체 시행 중 성공의 횟수에 따른 확률변수
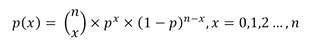

시행횟수 n은 자연수이며, 성공확률 p는 0 <= p <= 1을 만족
#이항분포
from elice_utils import EliceUtils
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from scipy import stats
elice_utils = EliceUtils()
# Q1. 이항분포 pmf 그리기
## 이항분포 생성
n, p = 10, 0.3
stat_bin = sp.stats.binom(n, p)
## 그리기
fig, ax = plt.subplots()
## pmf를 만드는 코드를 작성해 주세요
x_axis = np.arange(n + 1)
plt.bar(x_axis, stat_bin.pmf(x_axis))
##
plt.show()
fig.savefig("pmf_plot.png")
elice_utils.send_image("pmf_plot.png")
# Q2. 이항분포 cdf 그리기
## cdf 만드는 코드를 작성해 주세요
x_axis = np.arange(n + 1)
plt.bar(x_axis, stat_bin.cdf(x_axis))
##
plt.show()
fig.savefig("cdf_plot.png")
elice_utils.send_image("cdf_plot.png")
# Q3. 랜덤표본 추출
## seed 설정 seed=0
np.random.seed(seed=0)
## 랜덤 샘플 추출
random_bin = np.random.binomial(n=10, p=0.3, size=50)
print(random_bin)
## 평균계산
bin_mean = np.mean(random_bin)
print(bin_mean)
-초기하분포
유한한 모집단에서 비복원 추출 시, 성공의 횟수의 분포
X:표본 내에서 관심있는 범주 (ex: 불량품 개수)에 속하는 구성원소의 수
불량률 계산 등에서 많이 사용
X ~ Hyper(M, n, N)
모집단의 크기가 M, 표본의 크기가 N, 관심있는 범주 (ex 불량품 개수)에 속하는 구성원소의 수가 n

#초기하분포
from elice_utils import EliceUtils
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from scipy import stats
elice_utils = EliceUtils()
# Q1. 초기하분포 pmf 그리기
## 초기하분포 생성
[M, n, N] = [30, 5, 10]
stat_hyp = sp.stats.hypergeom(M, n, N)
## 그리기
fig, ax = plt.subplots()
## pmf를 만드는 코드를 작성해 주세요
x_axis = np.arange(n + 1)
plt.bar(x_axis, stat_hyp.pmf(x_axis))
##
plt.show()
fig.savefig("pmf_plot.png")
elice_utils.send_image("pmf_plot.png")
# Q2. 초기하분포 cdf 그리기
## cdf 만드는 코드를 작성해 주세요
x_axis = np.arange(n + 1)
plt.bar(x_axis, stat_hyp.cdf(x_axis))
##
plt.show()
fig.savefig("cdf_plot.png")
elice_utils.send_image("cdf_plot.png")
# Q3. 랜덤표본 추출
## seed 설정 seed=0
np.random.seed(seed=0)
## 랜덤 샘플 추출
random_hyp = np.random.hypergeometric(ngood=5, nbad=25, nsample=10, size=50)
print(random_hyp)
## 평균계산
hyp_mean = np.mean(random_hyp)
print(hyp_mean)
-포아송 분포
시행횟수가 많고 순간의 성공확률은 작기 때문에 이항분포로 설명하기 어려움
단위시간 / 공간에 드물게 나타나는 사건의 횟수에 대한 확률분포
ex) 일정 시간 동안 톨게이트를 지나는 차량의 수

B(n,p)에서 n이 매우 크고 p가 매우 작은 경우 람다 = np인 포아송 분포로 근사 가능
-균일 분포
구간 [a, b]에 속하는 값을 가질 수 있고 그 확률이 균일한 분포


#균일분포
from elice_utils import EliceUtils
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from scipy import stats
elice_utils = EliceUtils()
# Q1. 균일분포 pmf 그리기
## 균일분포 생성
stat_uni = sp.stats.uniform(0, 1)
# 그리기
fig, ax = plt.subplots()
## pdf를 만드는 코드를 작성해 주세요
x_axis = np.linspace(0, 1, 100)
plt.bar(x_axis, stat_uni.pdf(x_axis))
##
plt.show()
fig.savefig("pdf_plot.png")
elice_utils.send_image("pdf_plot.png")
# Q2. 균일분포 cdf 그리기
## cdf 만드는 코드를 작성해 주세요
x_axis = np.linspace(0, 1, 100)
plt.bar(x_axis, stat_uni.cdf(x_axis))
##
plt.show()
fig.savefig("cdf_plot.png")
elice_utils.send_image("cdf_plot.png")
# Q3. 균일분포 샘플링
## seed 설정
np.random.seed(seed=0)
## 샘플 추출
random_uni = np.random.uniform(0, 1, 100)
print(random_uni)
## 평균 계산
uni_mean = np.mean(random_uni)
print(uni_mean)
-정규분포

-표준정규분포

#정규분포
from elice_utils import EliceUtils
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from scipy import stats
elice_utils = EliceUtils()
# Q1. 정규분포 pdf 그리기
## 정규분포 생성
stat_nor = sp.stats.norm(0,1)
## 그리기
fig, ax = plt.subplots()
## pdf를 만드는 코드를 작성해 주세요
x_axis = np.linspace(-3, 3, 100)
plt.bar(x_axis, stat_nor.pdf(x_axis))
##
plt.show()
fig.savefig("pdf_plot.png")
elice_utils.send_image("pdf_plot.png")
# Q2. 정규분포 cdf 그리기
## cdf 만드는 코드를 작성해 주세요
x_axis = np.linspace(-3, 3, 100)
plt.bar(x_axis, stat_nor.cdf(x_axis))
##
plt.show()
fig.savefig("cdf_plot.png")
elice_utils.send_image("cdf_plot.png")
# Q3. 정규분포 샘플링
## seed 설정
np.random.seed(seed=0)
## 샘플 추출
random_nor = np.random.normal(0, 1, 100)
print(random_nor)
## 평균 계산
nor_mean = np.mean(random_nor)
print(nor_mean)
모집단과 표본
모집단의 일부를 표본으로 추출하여 표본으로 모집단의 정보를 추론/추정함
통계적 추론
표본이 갖고 있는 정보를 분석하여 모수를 추론
표본으로 전체 모집단의 성질을 추론하므로 오류 존재 (이 부정확도를 반드시 언급해야함)
모수추정
-모수에 대한 추론 혹은 추론치 제시
-수치화된 정확도 제시
가설검정
-모수에 대한 여러 가설들이 적합한지 표본으로 판단
모수 추정
-점추정

-구간추정
신뢰구간: 추정량의 분포를 이용하여 표본으로부터 모수의 값을 포함하리라 예상되는 구간
신뢰수준: 신뢰구간이 모수를 포함할 확률을 1보다 작은 일정한 수준에서 유지할 때 확률
모평균 구간추정
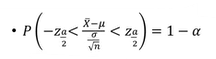
가설검정
모집단의 특성이나 모수에 대한 주장이 있을 때, 이 주장의 옳고 그름을 표본자료를 이용하여 판단하는 방법
귀무가설: H0 기본적인 가설
대립가설: H1 자료를 통하여 입증하고자 하는 가설, 비교하고 싶은 가설
통계적 가설 검정
설정한 가설에 대한 옳고 그름을 표본자료를 통하여 검정, 두 가설 중 옳다고 판단할 수 있는 하나의 가설을 선택
대립가설을 채택: 귀무가설 H0기각
귀무가설 채택: 귀무가설 H0 기각 불가능 or 귀무가설 H0 채택
오류의 종류

1종 오류를 범할 때 더 큰 손실이나 비용이 발생하는 경우가 많음
제 1종 오류 범할 확률을 우선 최소화하기
유의수준
제 1종으의 오류를 범할 확률에 대한 최대 허용한계 고정값
가설검정과정
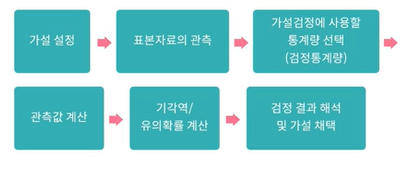
검정통계량
가설검정에 사용되는 통계량
1. 기각역
X가 취하는 구간 중에서 H0를 기각하는 구간

2. 유의확률 (p-value)
표본자료가 대립가설을 지지하는 정도를 0과 1사이의 숫자로 나타낸 최소의 유의수준 값
이항검정
이항분포를 이용하여 베르누이 확률변수의 모수 p에 대한 가설 조사
모평균 가설검정
표본의 크기가 클 때, 모평균이 정규분포를 따른다는 가정하에 중심극한정리에 의해 정규분포에 근사함

#이항검정
import numpy as np
import scipy as sp
from scipy import stats
# 이항 검정
## seed 설정 seed = 0
np.random.seed(seed = 0)
## 샘플 추출
random_ber = np.random.binomial(n=1, p=0.5, size=50)
print(random_ber)
n_ber = np.count_nonzero(random_ber)
print(n_ber)
## 가설 검정
binom_test = sp.stats.binom_test(n_ber, 50)
print(binom_test)
#모평균 가설검정
import numpy as np
import scipy as sp
from scipy import stats
# 모평균 가설검정
## seed 설정 seed = 0
np.random.seed(seed = 0)
## 샘플 추출
random_nor = np.random.normal(100,5,10)
print(random_nor)
## 평균 계산
nor_mean = np.mean(random_nor)
print(nor_mean)
## 모평균 가설 검정 함수 정의
def ztest(stat, mu, sigma):
z = (stat.mean() - mu) / (sigma / np.sqrt(len(stat)))
return (2 * (1 - sp.stats.norm.cdf(z)))
## 모평균 가설 검정
mu_test = ztest(random_nor, 100, 5)
print(mu_test)'[데이터분석] > Python | AI | 머신러닝' 카테고리의 다른 글
| Classification Problem (0) | 2024.09.10 |
|---|---|
| Regression Problem (0) | 2024.09.09 |
| Python을 활용한 프로그래밍 확률통계_Part 3 (0) | 2024.07.30 |
| 현업 문제해결 유형별 머신러닝 알고리즘 Part 1 (0) | 2024.07.29 |
| 실무 중심의 데이터 분석 방법 Part.4 (0) | 2024.07.29 |