Loss Function
모델의 성능을 측정하는, 모델이 얼마나 잘 학습할 수 있는지
좋은 알고리즘 기준
-Set of rules to obtain the expected output from given input
-Quality of Expected output
-새로운 데이터를 input 했을 때, 얼마나 정확히 예측했는가
-Error가 낮아야 함
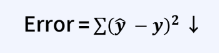
Error = Variance + Bias
-variance: 추정값의 평균과 추정값들간의 차이
-bias: 추청값의 평균과 참값들의 차이
-bias는 참 값과 추정 값의 거리를 의미, variance는 추정 값들의 흩어진 정도를 의미함
-low bias, low variance가 best 모델임
Error(X) = Noise(X) + Bias(X) + Variance(X)
Simple Linear Regression
독립변수X 1개, 종속변수Y 1개
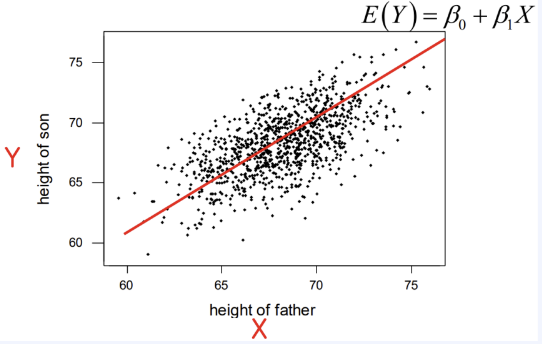
Multi Linear Regression
독립변수X 여러개, 종속변수Y 1개

β(계수) 추정 법
-각 β에 대해 편미분을 사용하여 추정을 사용함
-β가 여러개일 때 똑같이 각 β에 대해 미분 수행 후 추정함
추정한 β에 대해 검증을 수행: 귀무가설 vs 대립가설
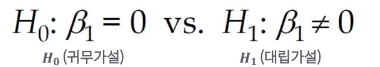
H0: 평균으로 되어버림. Y에 어떠한 영향도 미치지 않는 것으로 나타나버림
- β에 대한 p-value가 낮으면 기울기가 0이 아닌 것으로 판명 (H1채택)
-보통 p-value 0.05 기준으로 사용함
X들 간 중요한 변수를 ranking 하고 싶을 때는 어떻게...?
ex) 키와 몸무게는 기본적으로 scale이 다르기 때문에 x들 간 상대적인 비교는 불가능함
→ scaling 수행
1. p-value 먼저 체크
< 0.05 변수 전부 select
2. β의 크기를 확인하기
3. β가 동일할 경우 p-value가 낮은 변수가 중요한 변수라고 해석하기
'[데이터분석] > Python | AI | 머신러닝' 카테고리의 다른 글
| Python을 활용한 프로그래밍 확률통계_Part 4 (0) | 2024.08.01 |
|---|---|
| Python을 활용한 프로그래밍 확률통계_Part 3 (0) | 2024.07.30 |
| 실무 중심의 데이터 분석 방법 Part.4 (0) | 2024.07.29 |
| Python을 활용한 프로그래밍 확률통계_Part 2 (0) | 2024.07.29 |
| 실무 중심의 데이터 분석 방법 Part.3 (0) | 2024.07.28 |