그림이나 도표에 의한 분석의 단점
-작성자의 주관적 판단에 따라 달라지므로 일관성 및 객관성이 부족
-시각적 자료는 이론적 근거 제시가 쉽지 않음
→ 많은 양의 자료를 의미 있는 수치로 요약하여 대략적인 분포 상태를 파악 가능하므로 단점 보완 가능
수치를 통한 연속형 자료 요약
1) 중신 위치의 측도
2) 퍼진 정도의 측도
3) 도수분포표에서의 자료의 요약
4) 상자 그림
중심위치의 측도
-평균
-중앙값
-최빈값
평균
np.mean()
중심위치의 측도 중에서 가장 ㅁ낳이 사용되는 방법
모든 관측값의 합을 자료의 개수로 나눈 것
관측값들의 무게 중심
-관측값의 산술평균으로 사용
-통계에서 기초적인 통계 수치로 가장 많이 사용
-극단적으로 큰 값이나 작은 값의 영향을 많이 받음
중앙값
np.median()
전체 관측값을 정렬했을 때 가운데에 위치하는 값

-관측값을 크기 순서대로 배열할 때 중앙에 위치
-가운데에 위치한 값 이외의 값의 크기는 중요하지 않음
-관측값의 변화에 민감하지 않고, 극단값의 영향을 받지 않음
최빈값
stats.mode()
관측값 중 가장 자주 나오는 값
이산형 / 범주형 자료에서 많이 사용
-연속형 자료에서 같은 값이 나오는 경우는 흔치 않으므로 최빈값을 사용하기 부적절
-단봉형 분포를 갖는 자료에서만 유용
#중심위치의 측도: 평균
import numpy as np
from scipy import stats
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 평균 계산
cf_mean = np.mean(coffee)
print("Mean :", round(cf_mean, 2))#중심위치의 측도: 중앙값
import numpy as np
from scipy import stats
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 중앙값 계산
cf_median = np.median(coffee)
print("Median :", round(cf_median, 2))#중신위치의 측도: 최빈값
import numpy as np
from scipy import stats
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 최빈값 계산
cf_mode = stats.mode(coffee)
print("Mode :", cf_mode[0][0])
평균
-이해하기 쉽고 통계적으로 가장 많이 사용
-관측값이 골고루 반영
-극단값으로 인한 영향을 많이 받음
중앙값
-중앙 부분 외 관측값의 변화에 민감하지 않음
-극단값으로 인한 영향을 받지 않음

퍼진 정도의 측도
중심 위치만으로 분포를 파악하기에 부족
→ 중심위치 측도 외에 분포가 퍼진 정도를 측도할 수치가 필요
→ 분산, 표준편차, 범위, 사분위수 등을 퍼진 정도의 측도로 사용
분산
variance()
자료가 얼마나 흩어졌는지 숫자로 표현
각 관측값이 자료의 평균으로부터 떨어진 정도


편차의 제곱의 평균으로 퍼진 정도를 측정할 수 있다

표준편차
stdev()
분산의 단위 = 관측값의 단위의 제곱
→ 관측값의 단위와 불일치
분산의 양의 제곱근은 관측값과 단위가 일치
→ 분산의 양의 제곱근을 표준편차라 하고 s로 표기
#퍼진 정도의 측도: 분산
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 분산 계산
cf_var = variance(coffee)
print("Simple Variance :", round(cf_var, 2))#퍼진 정도의 측도: 표준편차
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 표준편차 계산
cf_std = stdev(coffee)
print("Sample std.Dev : ", round(cf_std, 2))
범위와 백분위수
범위
np.max() - np.min()
관측값에서 가장 큰 값과 가장 작은 값의 차이
백분위수
np.percentile()
중앙값을 확장한 개념
자료를 순서대로 정렬했을 때 백분율로 특정 위치의 값을 표현

#퍼진 정도의 측도: 범위
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 범위 계산
cf_range = np.max(coffee, axis=0) - np.min(coffee, axis=0)
print("Range :", cf_range)#퍼진 정도의 측도: 백분위수
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# 백분위수
cf_quant_20 = np.percentile(coffee, 20)
cf_quant_80 = np.percentile(coffee, 80)
print("20 Quantiles : ", cf_quant_20)
print("80 Quantiles : ", cf_quant_80)
사분위수


#퍼진 정도의 측도: 사분위수 범위
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
#IQR
q75, q25 = np.percentile(coffee, [75, 25])
cf_IQR = q75 - q25
print("Inter quartile range:", cf_IQR)

변동계수
퍼진 정도를 상대적으로 나타내는 수치를 사용

비교 대상의 단위가 다른 경우, 단위가 없는 변동계수를 통해 퍼진 정도 비교 가능
#퍼진 정도의 측도: 변동계수
from statistics import variance, stdev
import numpy as np
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
# CV
cf_cv = stdev(coffee) / np.mean(coffee)
cf_cv = round(cf_cv, 2)
print("CV:", cf_cv)
도수분포표
자료가 도수분포표로 요약되고 원 자료는 주어지지 않을 경우
→ 계급구간의 모든 관측값이 계급의 중간값을 갖는다고 가정하여 평균과 분산을 계산
→ 원 자료를 그룹화에 의해 정보가 상실되기 때문에 가능하다면 원 자료를 이용


#수치형 자료의 요약: 도수분포표
import numpy as np
import pandas as pd
# 주량 데이터
drink_cup = pd.DataFrame({
"cup": [22, 7, 19, 3, 10, 8, 19, 7, 15, 9, 35, 5],
"who": ["A", "E", "D", "B", "C", "A", "A", "A", "D", "B", "C", "B"]
})
print(drink_cup)
# 도수분포표
factor_cup = pd.cut(drink_cup.cup, 4)
group_cup = drink_cup["cup"].groupby(factor_cup)
count_cup = group_cup.agg(["count"])
print(count_cup)
상자그림
plt.boxplot()
다섯가지 요약 수치 (최솟값, q1, q2, q3, 최댓값)을 그림으로 표현
일반적 그래프에선 드러나지 않는 수치를 함께 제공
제 1사분위수에서 제 3사분위수까지 상자로 그림
좌우에 선을 그어 최솟값, 최댓값을 나타냄
-상자-수염그림이라고도 함
-봉우리가 하나 있는 분포의 특징을 나타내는데 적절
#수치형 자료의 요약: 상자그림
from elice_utils import EliceUtils
import numpy as np
import matplotlib.pyplot as plt
elice_utils = EliceUtils()
#카페인 함유량
coffee = np.array([202, 177, 121, 148, 89, 121, 137, 158])
#상자그림
fig, ax = plt.subplots()
# 여기에 코드를 작성해주세요
plt.boxplot(coffee)
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("box_plot.png")
elice_utils.send_image("box_plot.png")
변수 자료의 요약
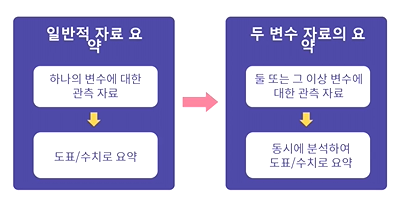
범주형 자료 - 분할표
수치형 자료 - 산점도, 공분산, 상관계수
분할표
도수분포표를 2차원으로 확장한 형태로 요약
두 변수의 범주들이 동시에 갖는 관측값의 수 (metrix)
pd.crosstab(index = 기준 범주, columns = 관측범주)
#두 범주형 변수의 요약: 분할표
import numpy as np
import pandas as pd
import matplotlib as plt
# 데이터 불러오기
mart = pd.read_csv("mart.csv")
print(mart)
# Q1.지역별로 선호하는 마트
region_crosstab = pd.crosstab(mart["region"], mart["mart"])
print(region_crosstab)
# Q2. 가족구성원의 수별로 선호하는 마트
famnum_crosstab = pd.crosstab(mart["family_num"], mart["mart"])
print(famnum_crosstab)
그림을 통한 두 연속형 변수의 요약: 산점도
plt.scatter(x = x 축 변수, y = y축 변수)
두 변수가 서로 어떤 관계인지 확인하기 위해 산점도를 사용
산점도 위의 점들의 경향 → 곡선 등 여러 가지 형태가 가능
#수치형 변수의 요약: 산점도
from elice_utils import EliceUtils
import matplotlib.pyplot as plt
import pandas as pd
elice_utils = EliceUtils()
# body.csv 읽어오기
body = pd.read_csv("body.csv")
# Q1. 산점도
# 1-1 키와 몸무게간 산점도
fig, ax = plt.subplots()
# 여기에 코드를 작성해 주세요
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("height_weight_plot.png")
elice_utils.send_image("height_weight_plot.png")
# 1-2 키와 체지방량 산점도
fig, ax = plt.subplots()
# 여기에 코드를 작성해 주세요
plt.scatter(body["height"], body["weight"])
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("height_fat_plot.png")
elice_utils.send_image("height_fat_plot.png")
# 1-3 키와 다리길이 산점도
fig, ax = plt.subplots()
# 여기에 코드를 작성해 주세요
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("height_leglen_plot.png")
elice_utils.send_image("height_leglen_plot.png")
# 1-4 키와 모발 산점도
fig, ax = plt.subplots()
# 여기에 코드를 작성해 주세요
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("height_hair_plot.png")
elice_utils.send_image("height_hair_plot.png")
공분산
dataframe.cov()
두 변수 (x,y)에 대해서 서로 어떤 관계를 가지는지 나타냄

두 변수의 편차를 곱하여 더한 후 자료의 개수 (N)으로 나누어줌
자료가 평균값으로부터 얼마나 멀리 떨어져 있는지 나타냄
#수치형 변수의 요약: 공분산
from statistics import variance, stdev
import numpy as np
import pandas as pd
# body.csv 읽어오기
body = pd.read_csv("body.csv")
# 공분산
cov_body = body.cov()
print(cov_body)
상관계수
산점도의 점들이 직선에 가까운 정도를 수치로 나타내어 관계를 파악
피어슨에 의해 제안되었기 때문에 피어슨의 상관계수라고도 불림
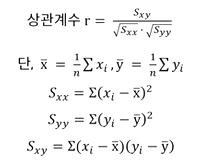
dataframe.corr()

r > 0: 두 변수의 값이 비례 관계를 나타냄
직선의 기울기는 양수
r < 0: 두 변수의 값이 반비례 관계를 나타냄
직선의 기울기는 음수
상관계수는 단위가 없음
상관계수만으로 판단 시 잘못된 해석 가능
인과관계: x가 y의 원인이 되고 있다고 믿어지는 관계
큰 상관계수 값이 항상 두 변수 사이의 인과관계를 의미하지는 않는다
#수치형 변수의 요약: 상관계수
from statistics import variance, stdev
import numpy as np
import pandas as pd
# body.csv 읽어오기
body = pd.read_csv("body.csv")
# 상관계수
corr_body = body.corr()
print(corr_body)
'[데이터분석] > Python | AI | 머신러닝' 카테고리의 다른 글
| 현업 문제해결 유형별 머신러닝 알고리즘 Part 1 (0) | 2024.07.29 |
|---|---|
| 실무 중심의 데이터 분석 방법 Part.4 (0) | 2024.07.29 |
| 실무 중심의 데이터 분석 방법 Part.3 (0) | 2024.07.28 |
| 실무 중심의 데이터 분석 방법 Part.2 (1) | 2024.07.26 |
| Python을 활용한 프로그래밍 확률통계_Part 1 (1) | 2024.07.22 |