자료의 형태
수치형 자료 (Numerical data) = 양적 자료 (Quantitative data)
수치로 측정이 가능한 자료
ex) 키, 몸무게, 시험 점수, 나이 등
→ 선형 회귀 분석 등 사용
범주형 자료 (Categorical data) = 질적 자료 (Qualitative data)
수치로 측정이 불가능한 자료
ex) 성별, 지역, 혈액형 등
→ 로지스틱 회귀 분석 등 사용
수치형 자료
연속형 자료 (Continuous data)
연속적인 관측값을 가짐
ex) 원주율, 시간 등
이산형 자료 (Discrete data)
셀 수 있는 관측값을 가짐
ex) 동영상 조회 수
범주형 자료와 수치 자료의 구분 != 자료의 숫자 표현 가능 여부
범주형 자료가 숫자로 표현되는 경우
: 남녀 성별 구분 시 남자를 1, 여자를 0으로 표현하는 경우, 숫자로 표현되어 있으나 범주형 자료
수치형 자료를 범주형 자료로 변환하는 경우
: 나이 구분 시, 나이 값은 수치형 자료지만 10~19세, 20~29세 등 나이 대에 따라 구간화 하면 범주형 자료
범주형 자료
순위형 자료 (Ordinal data)
범주 사이의 순서에 의미가 있음
ex) 학점
명목형 자료 (Nominal data)
범주 사이의 순서에 의미가 없음
ex) 혈액형
범주형 자료 요약
-각 범주에 속하는 관측값의 개수를 측정
-전체에서 차지하는 각 범주의 비율 파악
-효율적으로 범주 간의 차이점을 비교 가능
도수분포표
도수 (Frequency) 각 범주에 속하는 관측값의 개수 value_counts()
상대 도수 (Relative Frequency) 도수를 자료의 전체 개수로 나눈 비율 value_counts(normalize = True)
도수분포표 (Frequency Table) 범주형 자료에서 범주와 그 범주에 대응하는 도수, 상대도수를 나열해 표로 만든 것 pd.crosstab(index = 범주, columns = 또 다른 범주)
#범주형자료의 요약: 도수
import pandas as pd
import numpy as np
# drink 데이터
drink = pd.read_csv("drink.csv")
# 도수 계산
drink_freq = drink[drink["Attend"] == 1]["Name"].value_counts()
print("도수 계산")
print(drink_freq)#범주형 자료의 요약: 상대도수
import pandas as pd
import numpy as np
# drink 데이터
drink = pd.read_csv("drink.csv")
# 상대도수 계산
drink_relfreq = drink[drink["Attend"] == 1]["Name"].value_counts(normalize=True)
print("상대도수 계산")
print(drink_relfreq)#범주형 자료의 요약: 도수분포표
import pandas as pd
import numpy as np
# drink 데이터
drink = pd.read_csv("drink.csv")
# 전체 참석 횟수를 확인하는 도수분포표
drink_tab = pd.crosstab(index = drink["Attend"], columns = "count")
print("전체 참석 횟수를 확인하는 도수분포표")
print(drink_tab)
# 누가 몇 번 참석했는지 알 수 있는 도수분포표
drink_who = pd.crosstab(index = drink["Attend"], columns = drink["Name"])
print("누가 몇 번 참석했는지 알 수 있는 도수분포표")
print(drink_who)범주형 자료의 시각화
원형 그래프 (Pie Chart)
plt.pie(수치, labels = 라벨)
숫자의 나열보다 전체적인 분포를 이해하기 쉬운 그래프
장점: 전체 범주가 차지하는 비율을 파악하기 쉬움
단점: 범주 간 도수 비교 및 도수 크기 차이 파악이 어려움
막대 그래프 (Bar Chart)
plt.bar(x = 라벨, height = 수치)
각 범주에서 도수의 크기를 막대로 그림
장점: 각 범주가 가지는 도수의 크기 차이를 비교하기 쉬움
단점: 각 범주가 차지하는 비율의 비교는 어려움
#범주형 자료의 요약: 원형 그래프
from elice_utils import EliceUtils
import matplotlib.pyplot as plt
elice_utils = EliceUtils()
# 술자리 참석 상대도수 데이터
labels = ["A", "B", "C", "D", "E"]
ratio = [33,25,17,17,8]
# 원형 그래프
fig, ax = plt.subplots()
# Q1. 원형 그래프를 만드는 코드를 작성해 주세요
plt.pie(ratio,labels = labels)
plt.axis("equal")
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("pie_plot.png")
elice_utils.send_image("pie_plot.png")#범수형 자료의 요약: 막대그래프
from elice_utils import EliceUtils
import matplotlib.pyplot as plt
elice_utils = EliceUtils()
# 술자리 참석 상대도수 데이터
labels = ["A", "B", "C", "D", "E"]
ratio = [33,25,17,17,8]
# 막대 그래프
fig, ax = plt.subplots()
# Q1. 막대 그래프를 만드는 코드를 작성해 주세요
plt.bar(labels, ratio)
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("bar_plot.png")
elice_utils.send_image("bar_plot.png")수치형 자료의 요약
이산형 자료 요약
관측된 수치 자료가 셀 수 있는 경우 → 이산형 자료 요약
관측값의 종류가 많으면: 범주형 자료 요약 기법
관측값의 종류가 적으면: 연속형 자료 요약 기법
수치자료가 연속적으로 관측 → 연속형 자료 요약
관측값의 종류가 많으면: 연속형 자료 요약 기법
관측값의 종류가 적으면: 점도표, 도수분포표, 히스토그램, 상대도수다각형, 줄기-잎 그림
점도표 (dot diagram)
관측값의 개수가 상대적으로 적은 경우 (under 20 or 25) 사용
자료 전체의 개요를 파악 가능
모든 자료를 나타낼 수 있도록 줄 위에 각 관측값에 해당되는 점을 찍어 표시
도수분포표 (Frequency Table)
각 관측값에 대한 도수를 측정하여 도수분포표 작성
연속형 자료의 경우 다수의 구간 (계급)으로 나누고 각 구간마다 관측값의 개수(도수)로 작성
계급 (Class) / 계급구간 / 계급구간의 폭
-도수분포표 작성 순서
1. 자료의 범위 구하기
2. 계급의 폭 정하기
3. 계급 구간 경계점을 구하기
4. 계급의 도수를 더하기
5. 각 계급의 상대도수 구하기
히스토그램 (Histogram)
X축: 계급
Y축: 빈도
plt.hist()
연속형 자료의 도수분포표를 기반으로 각 계급을 범주처럼 사용
범주형 자료의 막대그래프와 같은 특징
-자료의 분포를 알 수 있음
-계급구간과 막대의 높이로 그림
-모든 계급구간의 폭이 같으면 도수, 상대도수를 막대 높이로 사용
도수다각형
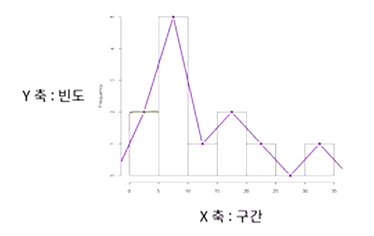
-각 계급구간의 중앙에 점을 찍어 직선으로 연결함
-관측값의 집중된 위치, 정도, 치우친 정도, 꼬리의 두터움 등 분포의 상태를 쉽게 파악
-관측값의 변화에 따라 도수 또는 상대도수의 변화를 잘 나타냄
히스토그램: 옆으로 나열하여 자료 비교
도수다각형: 꺾은선으로 표시
줄기-잎 그림
X축: 줄기
Y축: 잎
1. 관측값을 보고 앞 단위와 뒷 단위를 정함
2. 앞 단위를 줄기로 하여 세로로 배열하고 수직선을 그림
3. 뒷 단위를 잎으로 하여 관측값을 앞 단위 오른쪽에 오름차순 기입
plt.stem(줄기, 관측 값)
자료의 분포를 시각적으로 쉽게 파악
각 관측값도 유지 가능
장점: 관측값을 보여주므로 최댓값, 최솟값 등의 위치 파악 쉬움
: 순서대로 배열된 관측값의 장점과 히스토그램의 장점을 모두 가지고 있음
: 그리기 쉬움
단점: 관측값의 개수가 많은 경우 제한된 공간에 그리기 불가능
: 관측값이 지나치게 흩어져 있으면 부적절
#수치형 자료의 요약: 히스토그램
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from elice_utils import EliceUtils
elice_utils = EliceUtils()
# 주량 데이터
drink_cup = pd.DataFrame({
"cup": [22, 7, 19, 3, 10, 8, 19, 7, 15, 9, 35, 5],
"who": ["A", "E", "D", "B", "C", "A", "A", "A", "D", "B", "C", "B"],
"stems": [2, 0, 1, 0, 1, 0, 1, 0, 1, 0, 3, 0]
})
print(drink_cup)
fig, ax = plt.subplots()
# 히스토그램을 그리는 코드를 작성해 주세요
plt.hist(drink_cup["cup"])
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("hist_plot.png")
elice_utils.send_image("hist_plot.png")#수치형 자료의 요약: 줄기-잎 그림
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from elice_utils import EliceUtils
elice_utils = EliceUtils()
# 주량 데이터
drink_cup = pd.DataFrame({
"cup": [22, 7, 19, 3, 10, 8, 19, 7, 15, 9, 35, 5],
"who": ["A", "E", "D", "B", "C", "A", "A", "A", "D", "B", "C", "B"],
"stems": [2, 0, 1, 0, 1, 0, 1, 0, 1, 0, 3, 0]
})
print(drink_cup)
fig, ax = plt.subplots()
# 줄기-잎 그림을 그리는 코드를 작성해 주세요
plt.stem(drink_cup["stems"], drink_cup["cup"])
# 그래프를 그리는 코드입니다. 수정하지 마세요.
plt.show()
fig.savefig("stem_plot.png")
elice_utils.send_image("stem_plot.png")
'[데이터분석] > Python | AI | 머신러닝' 카테고리의 다른 글
| Python을 활용한 프로그래밍 확률통계_Part 2 (0) | 2024.07.29 |
|---|---|
| 실무 중심의 데이터 분석 방법 Part.3 (0) | 2024.07.28 |
| 실무 중심의 데이터 분석 방법 Part.2 (1) | 2024.07.26 |
| 실무 중심의 데이터 분석 방법 Part.1 (0) | 2024.07.16 |
| [DACON] 고객 대출등급 분류 기본 학습 (0) | 2024.02.27 |