Curse of Dimensionality
'차원의 저주'는 차원이 늘어남에 따라 같은 영역을 가지고 있음에도 전체 영역 대비 설명 가능한 데이터가 줄어들게 되는 현상
차원이 높아짐에 따라 어떠한 한 점이 나타내는 영역이 작아진다는 의미
(점 하나가 차원이 높아짐에 따라 설명력이 낮아짐)
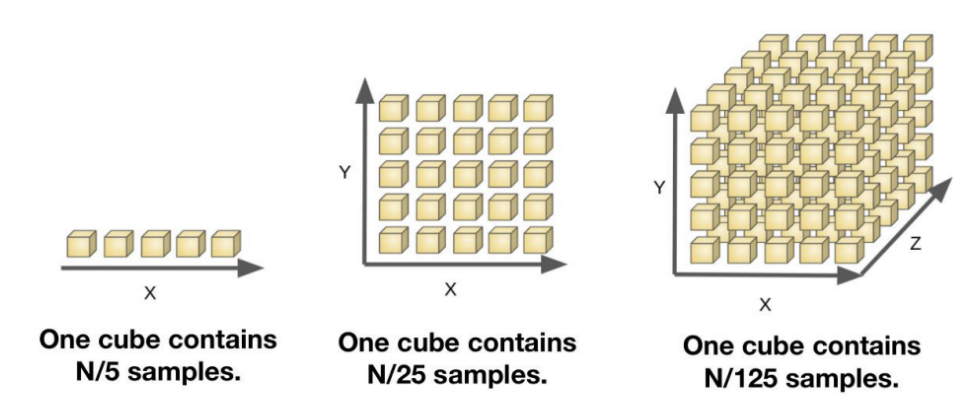
-고차원에 의한 저주 문제
Data 내 Noise를 가지고 있을 확률이 높아짐
학습할 때나 Model에 적용시킬 때 Computational Burden이 발생
Model이 예측할 때 많은 Data (차원적으로) 가 요구 됨
-고차원의 저주를 해결하는 방법
Domain Knowledge 사용
Regularization Term (Penalty Term)을 활용하여 Model이 학습 시 차원을 줄이는 방법 사용
Feature의 수를 새롭게 감소시키는 방법 사용
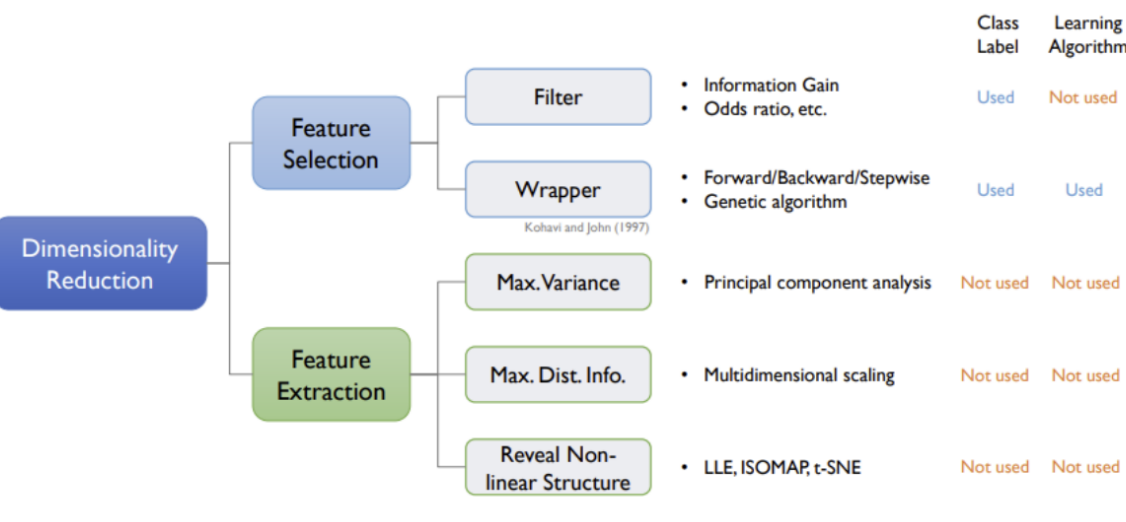
-지도학습을 통한 차원의 축소
Embedded: Regularized linear model, Random Forest using feature importance score
Filter: X's와 Y의 Correlation, Chi-squared Test, Anova, Variance inflation Factor
Wrapper: Forward Selection, Backward Elimination, Stepwise Selection
-비지도학습을 통한 차원의 축소
고차원에서의 Variance, Distance 등을 저차원에서도 그 정보를 그대로 보존할 수 있도록 학습함
비지도학습의 Best한 차원 축소는 고차원에서의 Data가 저차원에서의 Data와 똑같아야 함
Feature Extraction
LightGBM
Exclusive Feature Bundling (EFB)
step 1: Greedy Bundling: 어떤 Feature들을 하나로 Bundling할 것인지 탐색함
step 2: Merge Exclusive Features: 새로운 하나의 변수로 치환해 줌
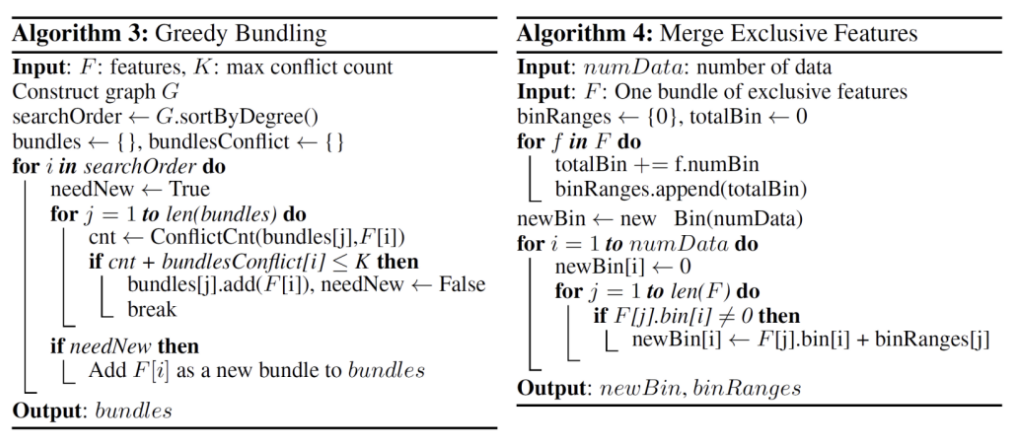
PCA
Principal Component Analysis
대표적인 Dimensionality Reduction에 쓰이는 기법 중 하나임
'고차원의 Data 분산도를 저차원에서도 얼마 만큼 잘 보존해주는가'를 모티브로 한 알고리즘
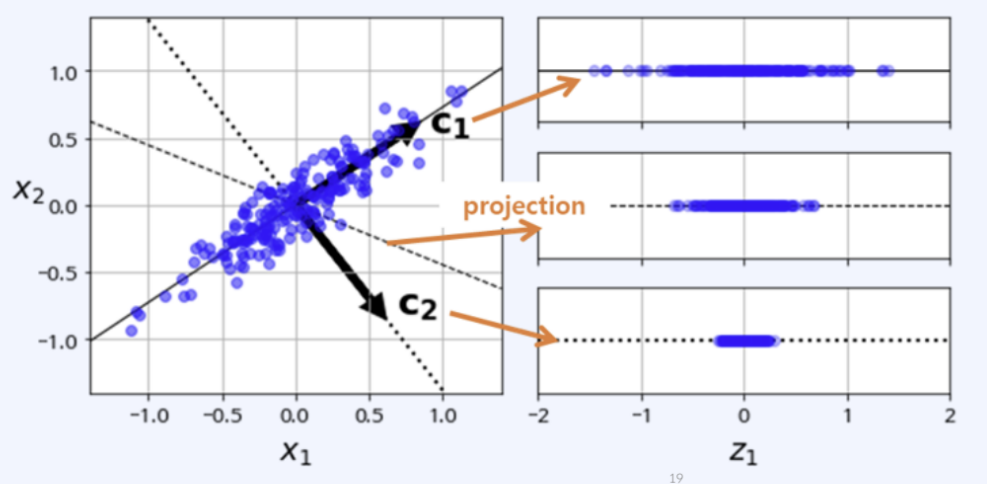
Covariance matrix: 시그마 기호로 표현하는 2차원 Data에서의 covariance matrix는 아래와 같음

eigenvector (고유벡터) : 공분산 행렬에 의해 선형변환 되는 수많은 vector들 중, 변환되기 전과 변환된 후의 vector 방햐잉 똑같은 vector를 의미함
변환된 수많은 Data 중 빨간색으로 표시된 벡터 2개만은 변환 전과 후의 방향이 동일함
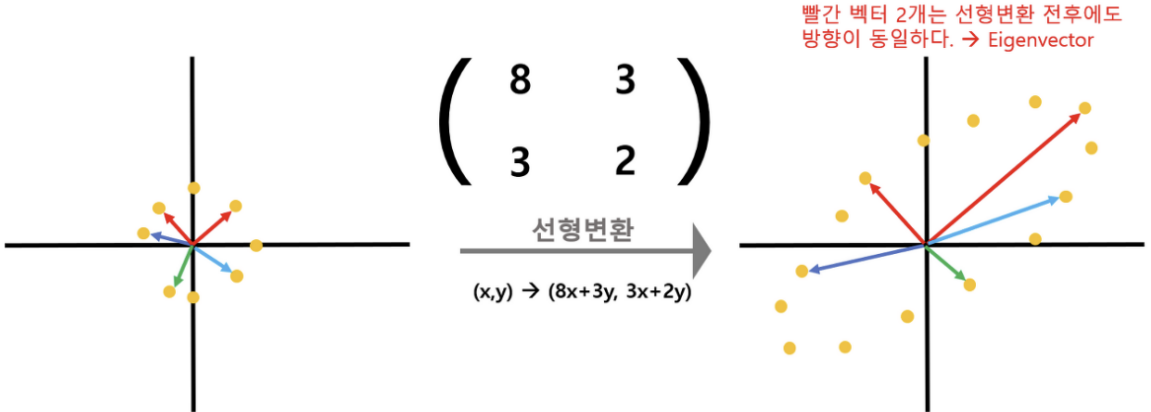
선형 변환이 되기 전과 후의 방향이 같은 벡터 v가 eigenvector, 변화되는 길이의 λ 비율 값이 eigenvalue
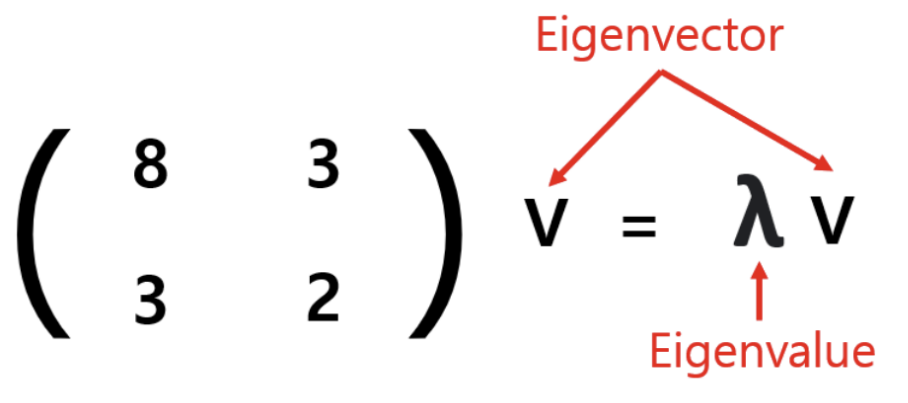
eigenvalue가 크면 클수록 고차원에서의 Data를 저차원에서 잘 표현한 것이라고 판단함
eigenvalue를 내림차순으로 정렬하고 가장 큰 N개 만큼 추출함
plotting 하기 위해 차원 축소를 진행한 것이라면 2~3개만 추출
T-SNE
T-distributed Stochastic Neighbor Embedding
높은 차원에서 비슷한 데이터 구조는 낮은 차원 공간에서 가깝게 대응하며, 비슷하지 않은 데이터 구조는 멀리 떨어져 있게 됨
비선형적인 차원 축소 방법 (특히 고차원의 Dataset을 시각화 하는 것에 굉장히 성능이 좋음)
고차원공간에서의 점들의 유사성과 그에 해당하는 저차원 공간에서의 점들의 유사성을 계산
점들의 유사도는 A를 중심으로 한 정규 분포에서 확률 밀도에 비례하여 이웃을 선택하면 포인트 A가 포인트 B를 이웃으로 선택한다는 조건부 확률로 계산
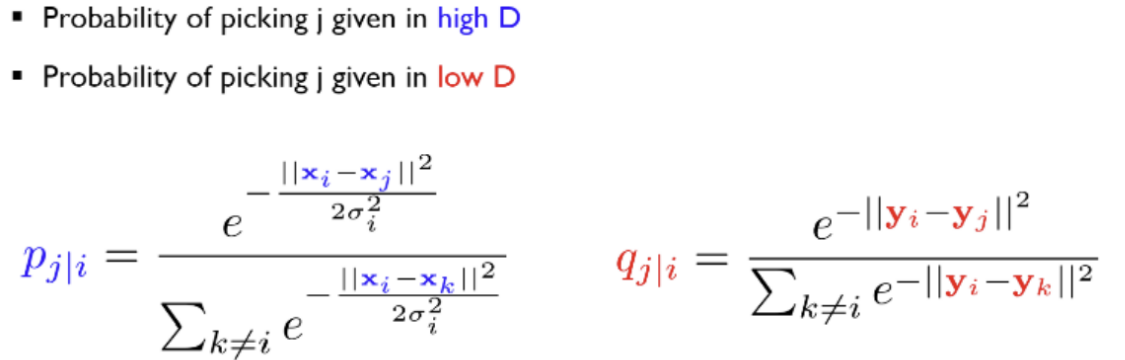
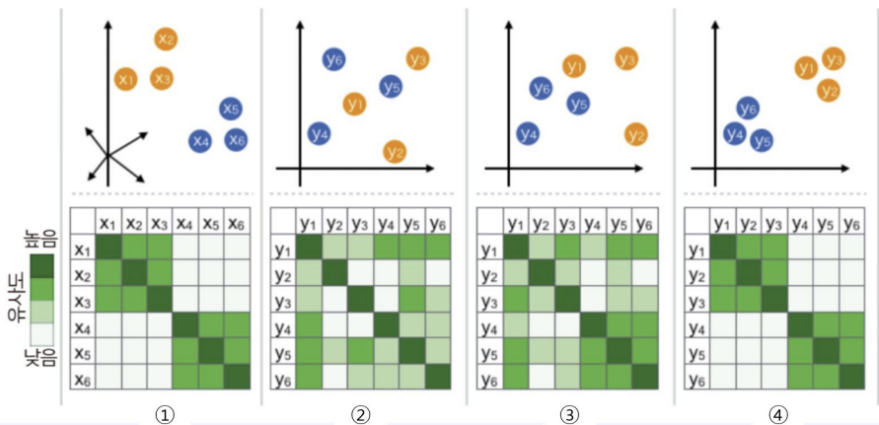
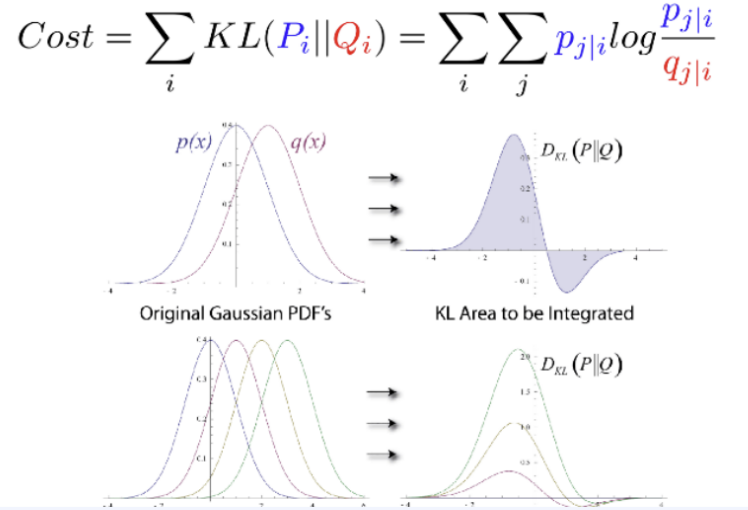
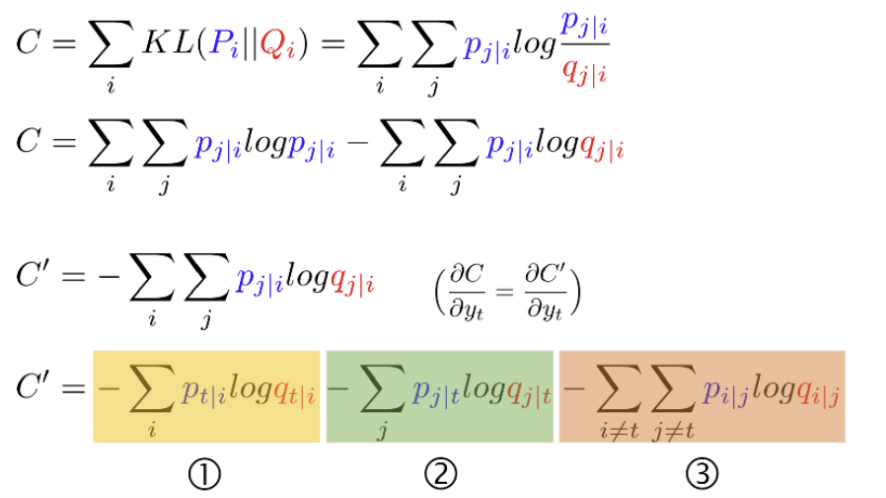
Kullback-Leibler divergence
두 확률분포의 차이를 계산하는 데 사용하는 함수로, 어떤 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산










Autoencoder
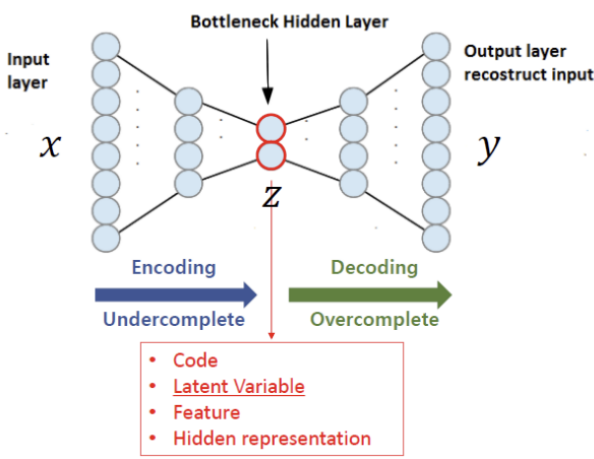
입력이 들어왔을 때, 해당 입력 데이터를 최대한 Compression 시킨 후, Compressed data를 다시 본래의 입력 형태로 복원시키는 신경망
Data를 압축하는 부분을 Encoder라고 하며 복원하는 부분을 Decoder라고 부름
압축 하는 과정에서 추출한 의미 있는 데이터 Z를 보통 Latent vector라고 부름
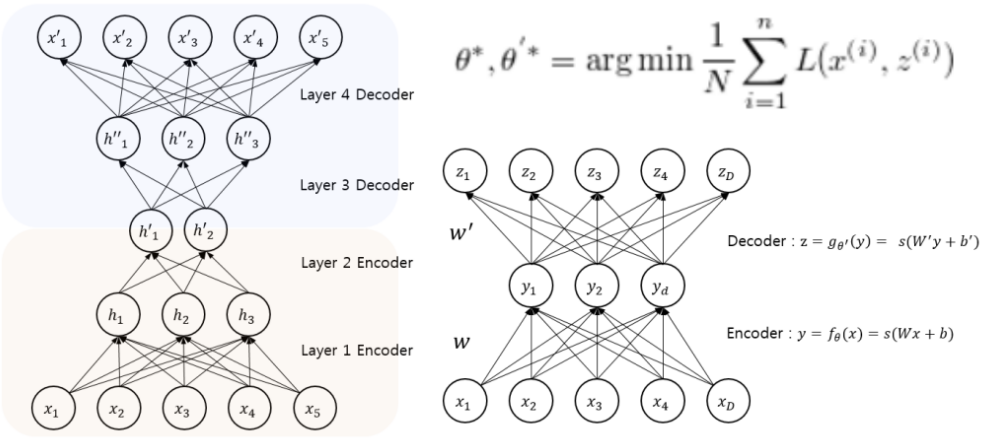
Gradient Descent 활용 Weight를 계속 update 시켜줌
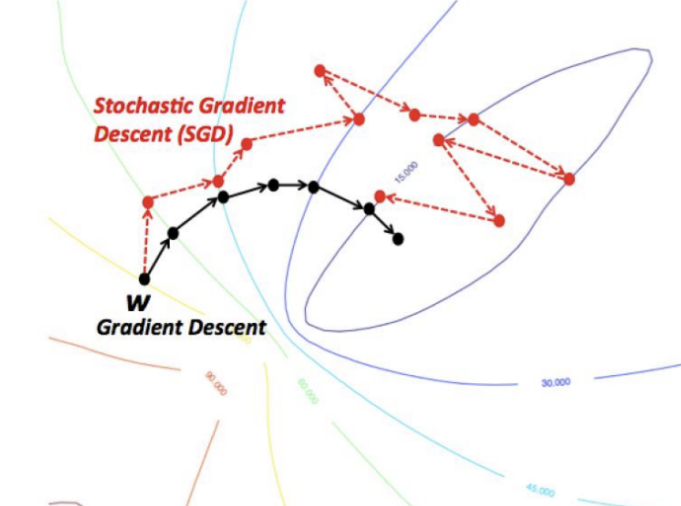
Layer의 Depth가 깊어지면 깊어질 수록 Gradient Vanishing or Exploding 현상이 발생하게 됨
Gradient Vanishing or Exploding은 역전파 (Backpropagation) 과정에서 마지막 Layer에서 멀어질 수록 Gradient 값이 매우 작아지거나 폭발하는 현상을 말함
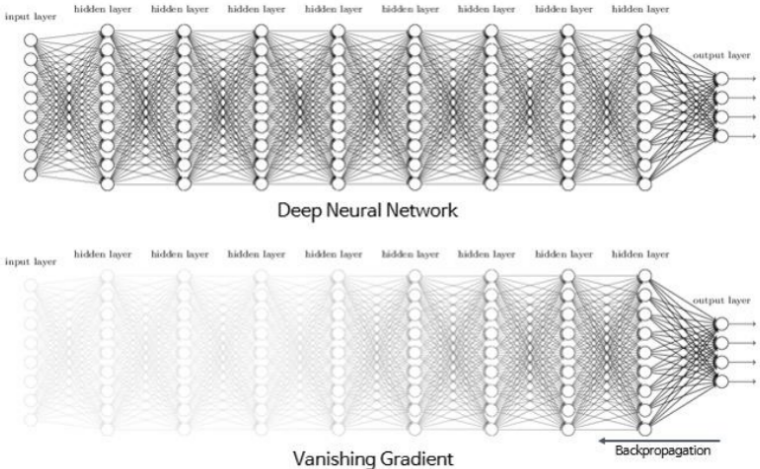
**Gradient Vanishing**(그래디언트 소실)과 **Gradient Exploding**(그래디언트 폭주)은 **인공 신경망(특히 딥러닝 모델)**을 학습할 때 발생하는 주요 문제들로, 주로 **역전파(Backpropagation)** 과정에서 등장합니다. 이들은 **신경망의 깊이**가 깊어질수록 자주 나타나며, 학습을 방해할 수 있는 중요한 문제입니다.
### 1. **Gradient Vanishing (그래디언트 소실)**
**그래디언트 소실**은 네트워크의 **가중치 업데이트를 위한 기울기(gradient)**가 점점 **0에 가까워지는 현상**을 말합니다. 주로 **깊은 신경망(Deep Neural Networks)**에서 발생하며, 이는 **역전파 과정**에서 기울기가 네트워크의 하위 계층으로 전달될 때 발생합니다.
#### 원인:
- 신경망에서 각 층의 가중치는 역전파를 통해 계산된 기울기에 의해 업데이트됩니다. 이때 기울기가 작은 값(예: 0에 매우 가까운 값)을 가지면, 역전파 과정에서 이러한 작은 값이 계속해서 곱해져 **앞쪽 레이어로 전달될수록 더 작아져** 결국 **기울기 값이 거의 0**에 가까워집니다.
- 특히 **시그모이드 함수**나 **하이퍼볼릭 탄젠트 함수(tanh)**와 같은 활성화 함수는 출력 값이 0에 가까운 구간에서 작은 기울기를 생성하므로, 이런 함수가 반복적으로 사용되면 기울기 소실 문제가 발생할 가능성이 높아집니다.
#### 결과:
- **가중치 업데이트**가 거의 일어나지 않습니다. 기울기가 0에 가까워지면 가중치가 거의 변하지 않으므로, 신경망이 **학습하지 못하는 상태**가 됩니다.
- 특히 **하위 층의 가중치**가 거의 업데이트되지 않아, 신경망의 하위 계층이 학습되지 않고, 네트워크가 효과적으로 성능을 내지 못하는 원인이 됩니다.
#### 해결책:
- **ReLU(Rectified Linear Unit)**와 같은 **비포화 활성화 함수**를 사용하는 것이 그래디언트 소실 문제를 완화할 수 있습니다. ReLU는 0 이상의 값에서 기울기가 1이므로, 기울기가 점점 줄어드는 문제를 방지할 수 있습니다.
- **Batch Normalization**: 각 층에서 입력 데이터를 정규화함으로써, 기울기가 너무 커지거나 작아지는 문제를 줄일 수 있습니다.
- **Residual Networks (ResNets)**: 깊은 네트워크에서 자주 사용되는 구조로, 입력이 다음 층으로 직접 전달되는 **스킵 연결**을 추가해 기울기가 소실되는 문제를 해결합니다.
---
### 2. **Gradient Exploding (그래디언트 폭주)**
**그래디언트 폭주**는 그래디언트 소실과는 반대로, 기울기 값이 **너무 커지는 현상**을 말합니다. 이 역시 **역전파 과정**에서 나타나며, 기울기가 앞쪽 레이어로 전달될 때 값이 기하급수적으로 커지는 경우입니다.
#### 원인:
- 각 층에서 기울기가 매우 큰 값을 가질 경우, 역전파 과정에서 계속해서 이러한 큰 값이 다음 층으로 곱해져 전달되면서 기울기가 **폭발적으로 증가**합니다.
- 이는 주로 **가중치가 무작위로 초기화**되거나, 특정 활성화 함수(예: **ReLU**에서의 매우 큰 출력)가 존재할 때 발생할 수 있습니다.
#### 결과:
- **가중치 업데이트**가 매우 큰 값으로 이루어지게 됩니다. 기울기 폭주가 발생하면 가중치가 지나치게 많이 변하게 되어, 네트워크가 **불안정**해지고 학습이 잘 이루어지지 않습니다.
- 손실 함수 값이 기하급수적으로 커지거나, 모델의 출력이 **NaN**이 되어 학습이 중단될 수 있습니다.
#### 해결책:
- **가중치 초기화 방법 개선**: He 초기화, Xavier 초기화와 같은 **적절한 가중치 초기화 방법**을 사용하여 초기 가중치 값을 안정적으로 설정하면 기울기 폭주를 방지할 수 있습니다.
- **Gradient Clipping**: 기울기의 크기를 일정 임계값으로 제한하는 기법입니다. 기울기가 너무 커지면, 임계값 이상으로는 더 이상 커지지 않도록 조정하여 기울기 폭주를 막습니다.
- **Batch Normalization**: 기울기 폭주를 방지하기 위해 각 층의 입력 데이터를 정규화함으로써 학습이 안정적으로 이루어지도록 도와줍니다.
---
### 요약:
1. **Gradient Vanishing** (그래디언트 소실):
- 기울기가 점점 0에 가까워지면서 가중치가 업데이트되지 않는 현상.
- 주로 깊은 네트워크에서 발생하며, 시그모이드 또는 tanh 활성화 함수에서 자주 나타남.
- 해결 방법: ReLU 활성화 함수, Batch Normalization, Residual Networks.
2. **Gradient Exploding** (그래디언트 폭주):
- 기울기가 지나치게 커지면서 가중치 업데이트가 불안정해지고, 손실 함수 값이 폭발적으로 증가하는 현상.
- 해결 방법: 적절한 가중치 초기화(He 초기화, Xavier 초기화), Gradient Clipping, Batch Normalization.
이 두 문제는 딥러닝에서 모델을 깊게 쌓을 때 자주 발생하는데, 이러한 문제를 해결하기 위한 기법들이 도입되면서 딥러닝 모델이 더 깊고 복잡해질 수 있었습니다.
'[데이터분석] > Python | AI | 머신러닝' 카테고리의 다른 글
| Anomaly Detection (0) | 2024.09.17 |
|---|---|
| Clustering (2) | 2024.09.16 |
| eXplainableMethod (1) | 2024.09.16 |
| Classification Problem (0) | 2024.09.10 |
| Regression Problem (0) | 2024.09.09 |